已知函数f(x)=x2-2|x-a| 若函数y=f(x)为偶函数,求a的值答案解析
科目:gzsx
来源:
题型:
已知函数
f(x)=为偶函数.
(Ⅰ)求实数a的值;
(Ⅱ)记集合E={y|y=f(x),x∈{-1,1,2}},
λ=lg22+lg2lg5+lg5-,判断λ与E的关系;
(Ⅲ)当x∈
[,](m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.
查看答案和解析>>
科目:gzsx
来源:山东省菏泽市2007-2008学年度高三第一学期阶段考试数学试题
题型:044
已知函数f(x)=ax4+bx3+cx2+dx+e为偶函数,它的图象过点A(0,-1),且在x=1处的切线方程为2x+y-2=0.
(1)求函数f(x)的表达式;
(2)若对任意x∈R,不等式f(x)≤t(x2+1)都成立,求实数t的取值范围.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知函数
f(x)=为偶函数.
(Ⅰ)求实数a的值;
(Ⅱ)记集合E={y|y=f(x),x∈{-1,1,2}},
λ=lg22+lg2lg5+lg5-,判断λ与E的关系;
(Ⅲ)当x∈
[,](m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知函数f(x)=|x-a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)与g(x)的图象在y轴上的截距相等.
(1)求a的值;
(2)若h(x)=f(x)+b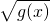 (b为常数),试讨论函数h(x)的奇偶性.
(b为常数),试讨论函数h(x)的奇偶性.
查看答案和解析>>
科目:gzsx
来源:2012年上海市卢湾区高考数学一模试卷(理科)(解析版)
题型:解答题
已知函数f(x)=|x-a|,g(x)=x
2+2ax+1(a为正常数),且函数f(x)与g(x)的图象在y轴上的截距相等.
(1)求a的值;
(2)若h(x)=f(x)+b

(b为常数),试讨论函数h(x)的奇偶性.
查看答案和解析>>
科目:gzsx
来源:2012年上海市卢湾区高考数学一模试卷(文科)(解析版)
题型:解答题
已知函数f(x)=|x-a|,g(x)=x
2+2ax+1(a为正常数),且函数f(x)与g(x)的图象在y轴上的截距相等.
(1)求a的值;
(2)若h(x)=f(x)+b

(b为常数),试讨论函数h(x)的奇偶性.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
为偶函数.
(Ⅰ)求实数a的值;
(Ⅱ)记集合E={y|y=f(x),x∈{-1,1,2}},λ=lg
22+lg2lg5+lg5-
,判断λ与E的关系;
(Ⅲ)若当x∈[
,
]时,n≤f(x)≤m恒成立,求m-n的最小值.
查看答案和解析>>
科目:gzsx
来源:2015-2016学年宁夏高二下期中文科数学试卷(解析版)
题型:解答题
已知函数f(x)=x2﹣2|x﹣a|
(1)若函数y=f(x)为偶函数,求a的值;
(2)若a= ,求函数y=f(x)的单调递增区间.
,求函数y=f(x)的单调递增区间.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•卢湾区一模)已知函数f(x)=|x-a|,g(x)=x
2+2ax+1(a为正常数),且函数f(x)与g(x)的图象在y轴上的截距相等.
(1)求a的值;
(2)若h(x)=f(x)+b
(b为常数),试讨论函数h(x)的奇偶性.
查看答案和解析>>
科目:gzsx
来源:河北省唐山一中2008-2009学年上学期高三期中考试(数学理)
题型:044
已知函数f(x)=ax4+bx3+cx2+dx+e(其中a,b,c,d,e∈R)为偶函数,它的图象过点A(0,-1),且在x=1处的切线方程为2x+y-2=0.
(1)求函数f(x)的表达式;
(2)若对任意x∈R,不等式f(x)≤t(x2+1)总成立,求实数t的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
为偶函数.
(1)求实数a的值;
(2)记集合E={y|y=f(x),x∈{-1,1,2}},λ=lg
22+lg2lg5+lg5-
,判断λ与E的关系;
(3)令h(x)=x
2f(x)+ax+b,若集合A={x|x=h(x)},集合B={x|x=h[h(x)]},若A=∅,求集合B.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=x2-2ax,把函数f(x)的图象向左平移1个单位,得到函数y=g(x)的图象.
(1)若g(x)为偶函数,求实数a的值;
(2)若2f(x)-g(x)+2(x-a)>0对于x∈[1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(Ⅰ)若当x=-1时函数y=g(x)取得极值,确定y=g(x)的单调区间
(Ⅱ)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax4+bx3+cx2+dx+e(其中a、b、c、d、x∈R)为偶函数,它的图象过点A(0,-1),且在x=1处的切线方程为2x+y-2=0.
(1)求a、b、c、d、e的值,并写出函数f(x)的表达式;
(2)若对任意x∈R,不等式f(x)≤t(x2+1)总成立,求实数t的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)同时满足如下三个条件:①定义域为[-1,1];②f(x)是偶函数;③x∈[-1,0]时,
f(x)=-,其中a∈R.
(Ⅰ)求f(x)在[0,1]上的解析式,并求出函数f(x)的最大值;
(Ⅱ)当a≠0,x∈[0,1]时,函数
g(x)=(+x-2-)[e2x-f(x)],若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
查看答案和解析>>
科目:gzsx
来源:
题型:
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=-1时函数y=g(x)取得极值,确定y=g(x)的单调区间.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax4+bx3+cx2+dx+e(其中a、b、c、d、x∈R)为偶函数,它的图象过点A(0,-1),且在x=1处的切线方程为2x+y-2=0.
(1)求函数f(x)的表达式;
(2)若对任意x∈R,不等式f(x)≤t(x2+1)总成立,求实数t的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(Ⅰ)求实数b、c的值;
(Ⅱ)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(Ⅲ)若当x=-1时函数y=g(x)取得极值,确定y=g(x)的单调区间和极值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=x
2+bx+c(b,c∈R)为偶函数,如果点A(x,y)在函数f(x)的图象上,且点B(x,y
2+1)在g(x)=f(x
2+c)的图象上.
(1)求函数f(x)的解析式;
(2)设F(x)=g(x)-λf(x).是否存在实数λ,使F(x)在
(-∞,-)上为减函数,且在
[-,0)上为增函数?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
x
3+ax
2+bx-1的导函数f′(x)为偶函数,直线x-y-1=0是y=f(x)的一条切线.
(1)求a、b的值.
(2)若g(x)=-f(x)+x
2+4x,求g(x)的极值.
查看答案和解析>>

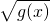 (b为常数),试讨论函数h(x)的奇偶性.
(b为常数),试讨论函数h(x)的奇偶性. (b为常数),试讨论函数h(x)的奇偶性.
(b为常数),试讨论函数h(x)的奇偶性. (b为常数),试讨论函数h(x)的奇偶性.
(b为常数),试讨论函数h(x)的奇偶性. ,求函数y=f(x)的单调递增区间.
,求函数y=f(x)的单调递增区间.