科目:czsx
来源:2015-2016学年江苏省八年级上第二次月考数学试卷(解析版)
题型:填空题
当x= 时,点A(4,x+2)与B(-3,6-3x)的连线平行于x轴.
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:022
当x=_________时,点A(4,x+2)与B(-3,6-3x)的连线平行于x轴.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
3.当x=1时,点A(4,x+2)与B(-3,6-3x)的连线平行于x轴.
查看答案和解析>>
科目:czsx
来源:
题型:
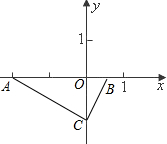
在平面直角坐标系内有两点A(-2,0),B(
,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:湖南省张家界市2006年初中毕业学业考试试卷数学
题型:044
在平面直角坐标系内有两点A(-2,0),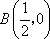 ,CB所在直线为y=2x+b,
,CB所在直线为y=2x+b,
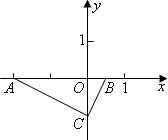
(1)求b与C的坐标
(2)连结AC,求证:△AOC∽△COB
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式
(4)在抛物线上是否存在一点P(不与C重合),使得S△ABP=S△ABC,若存在,请求出P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 在平面直角坐标系内有两点A(-2,0),B(
在平面直角坐标系内有两点A(-2,0),B( ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S△ABP=S△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:湖南省中考真题
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(
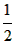
,0),CB所在直线为y=2x+b。
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S△ABP=S△ABC?若存在,请求出P点坐标;若不存在,请说明理由。
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
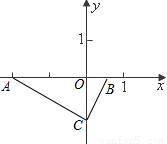
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
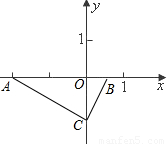
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(43):2.3 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(41):26.3 实际问题与二次函数(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(45):2.8 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(40):20.5 二次函数的一些应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(41):2.4 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(40):23.5 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2012年河北省石家庄市裕华区中考数学一模试卷(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2009-2010学年安徽省淮北市五校第二次联考九年级数学试卷(解析版)
题型:解答题
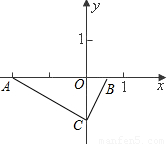
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(
,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC
∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线y=-
x
2+
x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:

如图,抛物线y=-
x
2-
x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(-3,0).
(1)求直线AB的函数关系式;
(2)动点E在线段OC上从原点出发以每秒一个单位的速度向C移动,过点E作EG⊥x轴,交直线AB于点F,交抛物线于点G.设点E移动的时间为t秒,GF的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点E与点O、C重合的情况),连接CF,BG,当t为何值时,四边形BCFG为平行四边形?问对于所求的t值,平行四边形BCFG是否菱形?请说明理由.
查看答案和解析>>

 在平面直角坐标系内有两点A(-2,0),B(
在平面直角坐标系内有两点A(-2,0),B(![]() ,CB所在直线为y=2x+b,
,CB所在直线为y=2x+b,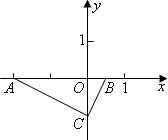
 在平面直角坐标系内有两点A(-2,0),B(
在平面直角坐标系内有两点A(-2,0),B( ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,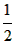 ,0),CB所在直线为y=2x+b。
,0),CB所在直线为y=2x+b。
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,


 如图,抛物线y=-
如图,抛物线y=-