过F作相互垂直的ABCD答案解析

科目：czsx 来源：单科王牌　　九年级数学(上) 题型：047

已知：如图所示，过ABCD的对角线交点O作相互垂直的两条直线EG、FH与ABCD的各边分别交于点E、F、G、H．

求证：四边形EFGH是菱形．

科目：gzsx 来源：2011-2012学年甘肃省高三百题集理科数学试卷（解析版）（四） 题型：解答题

科目：gzsx 来源：不详 题型：解答题

设点F(0,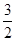),动圆P经过点F且和直线y=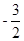相切，记动圆的圆心P的轨迹为曲线W.
⑴求曲线W的方程；⑵过点F作相互垂直的直线，，分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值；②分别在A,B两点作曲线W的切线，这两条切线的交点记为Q,求证：QA⊥QB,且点Q在某一定直线上。

科目：czsx 来源： 题型：解答题

3．如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论：（要求用文字语言叙述）垂美四边形两组对边的平方和相等
写出证明过程（先画出图形，写出已知、求证）．
（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．

科目：czsx 来源：三点一测丛书　九年级数学　上　（江苏版课标本） 江苏版课标本 题型：047

如图，过ABCD的对角线交点O作互相垂直的两条直线EG、FH与ABCD各边分别相交于点E、F、G、H．求证：四边形EFGH是菱形．

科目：czsx 来源：非常讲解·教材全解全析数学八年级上(配课标北师大版) 课标北师大版 题型：047

如图，过□ABCD的对角线交点O作互相垂直的两条直线EG、FH与平行四边形ABCD各边分别相交于点E、F、G、H．求证：四边形EFGH是菱形．

科目：czsx 来源：解题升级解题快速反应一典通八年级数学 题型：044

如图，过ABCD的对角线交点O作互相垂直的两条直线EG、FH，与平行四边形ABCD各边分别相交于点E、F、G、H，四边形EFGH是菱形吗？为什么？

科目：czsx 来源：新课标读想练八年级数学（上） 题型：047

如图，过ABCD对角线的交点O作两条互相垂直的直线EF、GH，分别与ABCD的四条边交于E、F和G、H，求证：EGFH为菱形．

科目：czsx 来源：新课标读想练八年级数学（上） 题型：047

如图，过ABCD对角线的交点O作两条互相垂直的直线EF、CH，分别与ABCD的四条边交于E、F和G、H，求证：EGFH为菱形．

科目：czsx 来源： 题型：

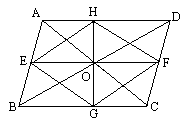
如图，过▱ABCD的对角线AC的中点O作互相垂直的两条直线，两直线分别与AB、BC、CD、DA相交于E、F、G、H四点，依次连接EF、FG、GH、HE，试判断四边形EFGH的形状，并说明理由．

科目：czsx 来源：数学课外练习八年级下学期使用 题型：047

如图，过□ABCD的对角线的交点O作两条互相垂直的直线EF、GH分别交□ABCD的四边于E、G、F、H．求证：四边形EGFH是菱形．

科目：czsx 来源：新课标读想练同步测试　八年级数学(下) 人教版 题型：047

已知：如图所示，过ABCD的对角线交点O作互相垂直的两条直线EG，FH与平行四边形ABCD各边分别相交于点E、F、G、H．求证：四边形EFGH是菱形．

科目：czsx 来源： 题型：047

科目：czsx 来源：中考必备’04全国中考试题集锦·数学 题型：047

证明题

已知：如图，过ABCD的对角线交点O作互相垂直的两条直线EG、FH与平行四边形ABCD各边分别相交于点E、F、G、H．求证：四边形EFGH是菱形．

科目：czsx 来源： 题型：

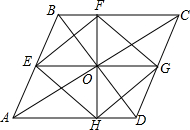过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线，分别交AB，BC，CD，DA于E，F，G，H四点，连接EF，FG，GH，HE．试判断四边形EFGH的形状，并说明理由．

科目：gzsx 来源： 题型：解答题

科目：czsx 来源： 题型：

如图，过平行四边形ABCD对角线的交点O作两条互相垂直的直线EF、GH分别交平行四边形ABCD四边于E、G、F、H，求证：四边形EGFH是菱形．

科目：czsx 来源： 题型：选择题

8．如图，过▱ABCD的对角线AC的中点O任作两条互相垂直的直线，分别交AB，BC，CD，DA于E，F，G，H四点，连接EF，FG，GH，HE，有下面四个结论，①OH=OF；②∠HGE=∠FGE；③S_{四边形DHOG}=S_{四边形BFOE}；④△AHO≌△AEO，其中正确的是（　　）

A．

①③

B．

①②③

C．

②④

D．

②③④

科目：czsx 来源： 题型：填空题

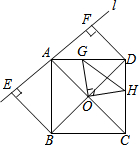11．如图直线l经过正方形ABCD的顶点A，分别过此正方形的顶点B、D作BE⊥l于点E，DF⊥l于点F．以正方形对角线的交点O为端点，引两条相互垂直的射线分别与AD、CD交于G、H两点，若EF=2，S_△ABE=$\frac{1}{2}$，则线段GH长度的最小值是1．

科目：gzsx 来源： 题型：解答题