科目：czsx 来源： 题型：
如图在△ABC中，D为BC上的一点，E为AD上的一点，BE的延长线交AC于点F，已知| BD |
| BC |
| 1 |
| a |
| AE |
| AD |
| 1 |
| b |
| AF |
| AC |
科目：czsx 来源： 题型：
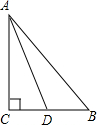如图在△ABC中∠C=90°，AD平分∠BAC交BC于D，若BC=64，且BD：CD=9：7，则点D到AB边的距离为（ ）| A、18 | B、32 | C、28 | D、24 |
科目：czsx 来源： 题型：
如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？ 科目：czsx 来源： 题型：
如图在△ABC中，AB=4，BC=4| 3 |
如图在△ABC中，∠B=40°，∠BCD=100°，EC平分∠ACB，求∠A与∠ACE的度数． 
如图在△ABC中，已知点D、E、F分别为边BC，AD，CE的中点，且△ABC的面积是4，则△BEF的面积是
如图在△ABC中，M是BC中点，AP是∠A平分线，BP⊥AP于P，AB=12，AC=22，则MP长为（ ）
如图在△ABC中，BD平分∠ABC且BD⊥AC于D，DE∥BC与AB相交于E．AB=5cm、AC=2cm，则△ADE的周长=
如图在△ABC中，点D是AB的中点，DC⊥AC，且tan∠BCD=
如图在△ABC中，两内角平分线交于一点E，∠A=70°，则∠E为（ ）
如图在△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE（垂足为D）交BC的延长线于点E，求线段CE的长． 
如图在△ABC中，已知∠B=45°，∠A=105°，AB=
如图在△ABC中，∠ACB=90°，CD⊥AB于D，AC=4，BC=3，则cos∠DCB=
如图在△ABC中∠A=70°，⊙O截△ABC的三条边所得的弦长相等，则∠BOC=（ ）
如图在△ABC中，∠ABC=50°，∠ACB=75°，点O是内心，则∠BOC的度数为
如图在△ABC中，点G是重心，连接BG并延长BG交AC于D，若点G到AB的距离为2，则点D到AB的距离是（ ）
如图在△ABC中，∠A=30°，∠ABC=105°，BD⊥AC于D点，BD=4．试求△ABC的周长． 
如图在△ABC中，AB=BC，D、E、F分别是BC、AC、AB边上的中点．