练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >如果ab为定值

    如果ab为定值答案解析

    科目：gzsx 来源： 题型：

    如图所示,如果α∥β,AB和AC是夹在平面α和β之间的两条线段,AB⊥AC,且AB=2,若直线AB与平面α所成的角为30°,能否确定线段AC的取值范围?若能,求出其范围;若不能,说明理由.

    查看答案和解析>>

    科目：czsx 来源： 题型：

    我们规定这样一种运算：如果ab=N（a＞0，N＞0），那么b就叫做以a为底的N的对数，记做b=logaN．例如：因为23=8，所以log28=3，那么log381的值为
    4
    4
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：单选题

    我们规定这样一种运算：如果ab=N（a＞0，N＞0），那么b就叫做以a为底的N的对数，记作b=logaN．例如：因为23=8，所以log28=3，那么log381的值为


    1. A.
      27
    2. B.
      9
    3. C.
      4
    4. D.
      381

    查看答案和解析>>

    科目：czsx 来源： 题型：填空题

    我们规定这样一种运算：如果ab=N（a＞0，N＞0），那么b就叫做以a为底的N的对数，记做b=logaN．例如：因为23=8，所以log28=3，那么log381的值为________．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：单选题

    我们规定这样一种运算：如果ab=N（a＞0，N＞0），那么b就叫做以a为底的N的对数，记作b=logaN．例如：因为23=8，所以log28=3，那么log381的值为（　　）
    A．27B．9C．4D．381

    查看答案和解析>>

    科目：czsx 来源：河北省期末题 题型：填空题

    我们规定这样一种运算：如果ab=N（a＞0，N＞0），那么b就叫做以a为底的N的对数，记做b=logaN．例如：因为23=8，所以log28=3，那么log381的值为 _________ ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    7、我们规定这样一种运算：如果ab=N（a＞0，N＞0），那么b就叫做以a为底的N的对数，记作b=logaN．例如：因为23=8，所以log28=3，那么log381的值为（　　）

    查看答案和解析>>

    科目：czsx 来源：2012年湖北省宜昌市中考适应性训练数学试卷（五）（解析版） 题型：解答题

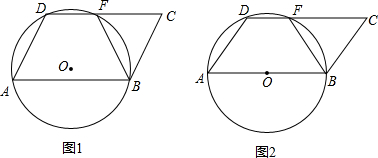
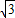    如图1，在▱ABCD中，AD=a，AB=a，a为定值，线段AD绕着点A旋转，旋转时∠DAB为锐角，经过A、D、B三点的圆⊙O和边CD相交于点F，点F不与点D重合．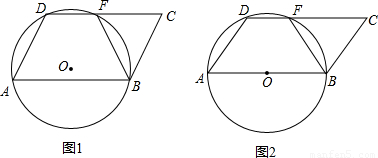
    （1）求∠DAB的范围；
    （2）如果AD旋转到使得AB刚好成为⊙O的直径（如图2所示），请你验证此时∠DAB的度数在第（1）问所求的范围内，并证明：此时点F恰好是DC的一个三等分点．

    查看答案和解析>>

    科目：czsx 来源：2008年湖北省宜昌市枝江市实验中学中考数学二模试卷（解析版） 题型：解答题

    如图1，在▱ABCD中，AD=a，AB=a，a为定值，线段AD绕着点A旋转，旋转时∠DAB为锐角，经过A、D、B三点的圆⊙O和边CD相交于点F，点F不与点D重合．
    （1）求∠DAB的范围；
    （2）如果AD旋转到使得AB刚好成为⊙O的直径（如图2所示），请你验证此时∠DAB的度数在第（1）问所求的范围内，并证明：此时点F恰好是DC的一个三等分点．

    查看答案和解析>>

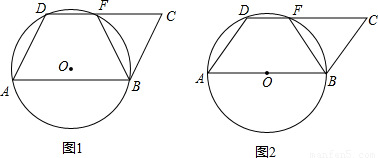
    科目：czsx 来源： 题型：

    如图1，在▱ABCD中，AD=a，AB=
    		3
    a，a为定值，线段AD绕着点A旋转，旋转时∠DAB为锐角，经过A、D、B三点的圆⊙O和边CD相交于点F，点F不与点D重合．
    （1）求∠DAB的范围；
    （2）如果AD旋转到使得AB刚好成为⊙O的直径（如图2所示），请你验证此时∠DAB的度数在第（1）问所求的范围内，并证明：此时点F恰好是DC的一个三等分点．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设两非零向量e1和e2不共线．
    （1）如果
    AB
    =e1+e2，
    BC
    =2e1+8e2，
    CD
    =3（e1-e2），求证：A、B、D三点共线；
    （2）试确定实数k，使ke1+e2和e1+ke2共线；
    （3）若|e1|=2，|e2|=3，e1与e2的夹角为60°，试确定k的值，使ke1+e2与e1+ke2垂直．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    如图1，在▱ABCD中，AD=a，AB=
    		3
    a，a为定值，线段AD绕着点A旋转，旋转时∠DAB为锐角，经过A、D、B三点的圆⊙O和边CD相交于点F，点F不与点D重合．
    （1）求∠DAB的范围；
    （2）如果AD旋转到使得AB刚好成为⊙O的直径（如图2所示），请你验证此时∠DAB的度数在第（1）问所求的范围内，并证明：此时点F恰好是DC的一个三等分点．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    设两非零向量e1和e2不共线．
    （1）如果
    AB
    =e1+e2，
    BC
    =2e1+8e2，
    CD
    =3（e1-e2），求证：A、B、D三点共线；
    （2）试确定实数k，使ke1+e2和e1+ke2共线；
    （3）若|e1|=2，|e2|=3，e1与e2的夹角为60°，试确定k的值，使ke1+e2与e1+ke2垂直．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如果把分式
    ab
    a+b
    中的a，b都扩大为原来的2倍，那么分式的值一定（　　）
    A、是原来的2倍
    B、原来的4倍
    C、是原来的
    1
    2
    D、不变

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如果规定符号“*”的意义是a*b=
    ab
    a+b
    ，则2*3*4的值为
    12
    13
    12
    13
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如果规定☆为一种运算符号，且a☆b=ab-ba，则4☆（3☆2）的值为（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如果多项式x2-7ab+b2+kab-1不含ab项，则k的值为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如果函数f（x）同时满足下列条件：①在闭区间[a，b]内连续，②在开区间（a，b）内可导且其导函数为f′（x），那么在区间（a，b）内至少存在一点ξ（a＜ξ＜b），使得f（b）-f（a）=f′（ξ）（b-a）成立，我们把这一规律称为函数f（x）在区间（a，b）内具有“Lg”性质，并把其中的ξ称为中值．有下列命题：
    ①若函数f（x）在（a，b）具有“Lg”性质，ξ为中值，点A（a，f（a）），B（b，f（b）），则直线AB的斜率为f′（ξ）；
    ②函数y=
    		2-
    x2
    2
    在（0，2）内具有“Lg”性质，且中值ξ=
    		2
    ，f′（ξ）=-
    		2
    2
    ；
    ③函数f（x）=x3在（-1，2）内具有“Lg”性质，但中值ξ不唯一；
    ④若定义在[a，b]内的连续函数f（x）对任意的x1、x2∈[a，b]，x1＜x2，有
    1
    2
    [f（x1）+f（x2）]＜f（
    x1+x2
    2
    ）恒成立，则函数f（x）在（a，b）内具有“Lg”性质，且必有中值ξ=
    x1+x2
    2
    ．
    其中你认为正确的所有命题序号是
     
    ．

    查看答案和解析>>

    科目：czsx 来源：2013年浙江省台州市高级中等学校招生考试数学 题型：044

    如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”

    (1)请用直尺与圆规画一个“好玩三角形”；

    (2)如图1，在Rt△ABC中，∠C＝90°，，求证：△ABC是“好玩三角形”；

    (3)如图2，已知菱形ABCD的边长为a，∠ABC＝2β，点P，Q从点A同时出发，以相同的速度分别沿折线AB－BC和AD－DC向终点C运动，记点P所经过的路程为S

    ①当β＝45°时，若△APQ是“好玩三角形”，试求的值

    ②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”请直接写出tanβ的取值范围．

    (4)本小题为选做题

    依据(3)中的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是“好玩三角形”的个数关系的真命题(“好玩三角形”的个数限定不能为1)．

    查看答案和解析>>

    科目：czsx 来源：2013年初中毕业升学考试（浙江台州卷）数学（带解析） 题型：解答题

    如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”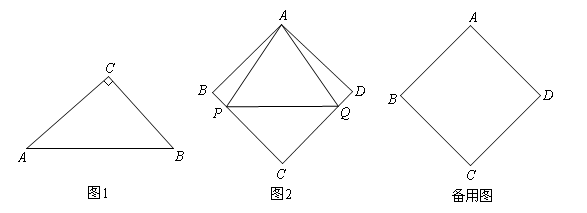

    （1）请用直尺与圆规画一个“好玩三角形”；
    （2）如图1，在Rt△ABC中，∠C=90°，，求证：△ABC是“好玩三角形”；
    （3）如图2，已知菱形ABCD的边长为a, ∠ABC=2β，点P，Q从点A同时出发，以相同的速度分别沿折线AB－BC和AD－DC向终点C运动，记点P所经过的路程为s
    ①当β=45°时，若△APQ是“好玩三角形”，试求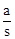的值；
    ②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”？请直接写出tanβ的取值范围。
    （4）本小题为选做题
    依据（3）中的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是“好玩三角形”的个数关系”的真命题（“好玩三角形”的个数限定不能为1）。

    查看答案和解析>>