如图.在△abc中.ab=bc.∠abc=90°.d为延长线上的一点答案解析
科目:czsx
来源:
题型:
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=
度;
(2)设∠BAC=α,∠BCE=β,∠BAC≠90°时
①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;
②当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明).

查看答案和解析>>
科目:czsx
来源:
题型:
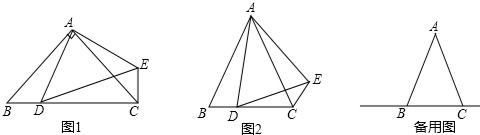
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC.设∠BAC=α,∠BCE=β.
(1)如图1,如果∠BAC=90°,∠BCE=
度;
(2)如图2,你认为α、β之间有怎样的数量关系?并说明理由.
(3)当点D在线段BC的延长线上移动时,α、β之间又有怎样的数量关系?请在备用图上画出图形,并直接写出你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
8.在△ABC中,AB=AC,点D是直线BC上一点(不与点B、点C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=90°;
(2)如图2,当点D在线段BC上时,如果∠BAC=50°,请你求出∠BCE的度数.(写出求解过程);
(3)探索发现,设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论:β=180°-α.
②当点D在线段BC的延长线上时,则α,β之间有怎样的数量关系?请在图3中画出完整图形并请直接写出你的结论:β=180°-α.

查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP.
(1)求证:∠BDP=2∠PBC;
(2)若∠EDP的平分线交BP的延长线于点F,求证:FC+FD=
BF.
查看答案和解析>>
科目:czsx
来源:
题型:
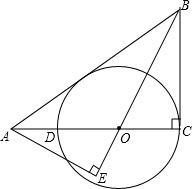
如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE
2=OE•BE.
(1)求证:AB是⊙O的切线;
(2)若BC=6,tan∠BAC=
,求AE的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
7.已知,在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B,C重合),连接AD,以AD为边作菱形ADEF,且∠DAF=∠BAC=α,连接CF,如图1,当点D在线段BC上时,我们易得CF、BC、CD三条线段之间的数量关系为:CF+CD=BC.
(1)如图2,当点D在线段BC的延长线上时,其他条件不变,请探究CF、BC、CD三条线段之间的数量关系并证明;
(2)如图3,当α=90°时,点D在线段BC的反向延长线上,且点A、F分别在直线BC的两侧,其他条件不变;
①请直接写出CF、BC、CD三条线段之间的数量关系;
②若菱形ADEF的边长为$\sqrt{2}$,对角线AE、DF相交于点O,连接OC,求OC的长.

查看答案和解析>>
科目:czsx
来源:
题型:
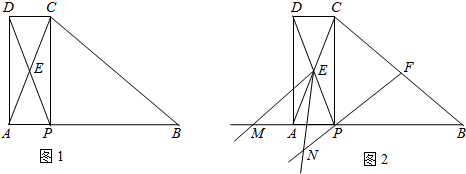
如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作▱APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
(1)求证:∠EAP=∠EPA;
(2)▱APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
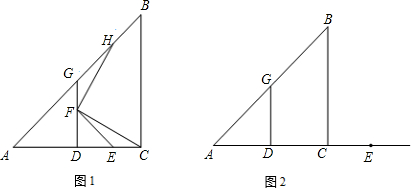
在Rt△ABC中,AC=BC,∠ACB=90°,D是AC的中点,DG⊥AC交AB于点G.
(1)如图1,E为线段DC上任意一点,点F在线段DG上,且DE=DF,连接EF与 CF,过点F作FH⊥FC,交直线AB于点H.
①求证:DG=DC;
②判断FH与FC的数量关系并加以证明.
(2)若E为线段DC的延长线上任意一点,点F在射线DG上,(1)中的其他条件不变,借助图2画出图形.在你所画图形中找出一对全等三角形,并判断你在(1)中得出的结论是否发生改变,(本小题直接写出结论,不必证明).
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE
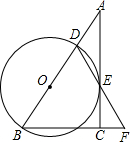
并延长,与BC的延长线交于点F,
(1)求证:BD=BF;
(2)当BC=3,AD=2时,求⊙O的面积;
(3)在(2)的条件下,判断△DBF是否为正三角形?并说明你的理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
(1)试说明:∠AEQ=90°;
(2)猜想EF与图中哪条线段相等(不能添加辅助线产生新的线段),并说明理由.
查看答案和解析>>
科目:czsx
来源:2010年福建省南安市初中学业质量检查数学试题
题型:044
如图,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
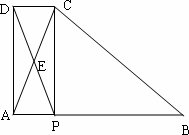
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:czsx
来源:福建省南平市2010年中考数学试题
题型:044
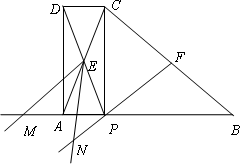
如图,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
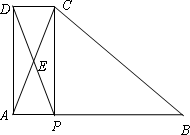
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:2007年陕西省初中毕业生学业考试数学模拟试卷(八)
题型:059
如下图,在△ABC中,∠C=90°,AC=6,BC=8,M是BC的中点,P为AB上的一个动点,(可以与A、B重合),并作∠MPD=90°,PD交BC(或BC的延长线)于点D.

(1)记BP的长为x,△BPM的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(2)是否存在这样的点P,使得△MPD与△ABC相似?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
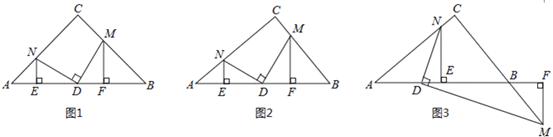
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
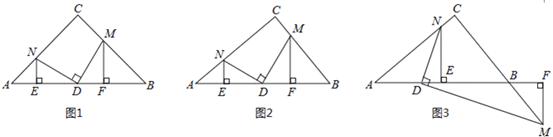
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。
查看答案和解析>>
科目:czsx
来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版)
题型:解答题
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。

查看答案和解析>>
科目:czsx
来源:
题型:解答题
在△ABC中,∠ACB为锐角,动点D(异于点B)在射线BC上,连接AD,以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)若AB=AC,∠BAC=90°那么
①如图一,当点D在线段BC上时,线段CF与BD之间的位置、大小关系是________(直接写出结论)
②如图二,当点D在线段BC的延长上时,①中的结论是否仍然成立?请说明理由.
(2)若AB≠AC,∠BAC≠90°.点D在线段BC上,那么当∠ACB等于多少度时?线段CF与BD之间的位置关系仍然成立.请画出相应图形,并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
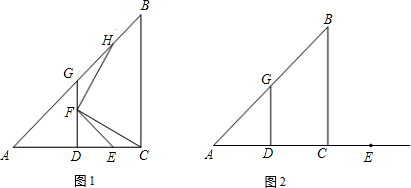
在Rt△ABC中,AC=BC,∠ACB=90°,D是AC的中点,DG⊥AC交AB于点G.
(1)如图1,E为线段DC上任意一点,点F在线段DG上,且DE=DF,连接EF与 CF,过点F作FH⊥FC,交直线AB于点H.
①求证:DG=DC;
②判断FH与FC的数量关系并加以证明.
(2)若E为线段DC的延长线上任意一点,点F在射线DG上,(1)中的其他条件不变,借助图2画出图形.在你所画图形中找出一对全等三角形,并判断你在(1)中得出的结论是否发生改变,(本小题直接写出结论,不必证明).
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F.
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F.
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
(1)试说明:∠AEQ=90°;
(2)猜想EF与图中哪条线段相等(不能添加辅助线产生新的线段),并说明理由.
查看答案和解析>>




 如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP.
如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP. 如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE.
如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE.


 并延长,与BC的延长线交于点F,
并延长,与BC的延长线交于点F, 如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.









 如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F.
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F. 如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.