科目:gzsx
来源:
题型:
已知下列命题:
①函数y=sin(-2x+
)的单调增区间是[-kπ-
,-kπ+
](k∈Z).
②要得到函数y=cos(x-
)的图象,需把函数y=sinx的图象上所有点向左平行移动
个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinωx(ω>0)在[0,1]上至少出现了100次最小值,则ω≥
π.
⑤函数y=lg(1-tanx)的定义域是(kπ-
,kπ+
)(k∈Z)
其中正确命题的序号是
.(将所有正确命题的序号都填上)
查看答案和解析>>
科目:gzsx
来源:
题型:
已知下列命题:
①函数y=sin(-2x+
)的单调增区间是[-kπ-
,-kπ+
](k∈Z).
②要得到函数y=cos(x-
)的图象,需把函数y=sinx的图象上所有点向左平行移动
个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④已知角A、B、C是锐角△ABC的三个内角,则点P(sinA-cosB,cosA-sinC)在第四象限.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年宁夏银川一中高三(上)第二次月考数学试卷(理科)(解析版)
题型:填空题
已知下列命题:
①函数

的单调增区间是

.
②要得到函数

的图象,需把函数y=sinx的图象上所有点向左平行移动

个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则

.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年宁夏银川一中高三(上)9月月考数学试卷(文科)(解析版)
题型:填空题
已知下列命题:
①函数

的单调增区间是

.
②要得到函数

的图象,需把函数y=sinx的图象上所有点向左平行移动

个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则

.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:《第1章 三角函数》2013年单元测试卷1(北京宏志中学)(解析版)
题型:填空题
已知下列命题:
①函数

的单调增区间是

.
②要得到函数

的图象,需把函数y=sinx的图象上所有点向左平行移动
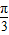
个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则

.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年宁夏银川一中高三(上)第二次月考数学试卷(理科)(解析版)
题型:填空题
已知下列命题:
①函数

的单调增区间是

.
②要得到函数

的图象,需把函数y=sinx的图象上所有点向左平行移动

个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则

.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年宁夏银川一中高三(上)9月月考数学试卷(文科)(解析版)
题型:填空题
已知下列命题:
①函数

的单调增区间是
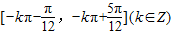
.
②要得到函数

的图象,需把函数y=sinx的图象上所有点向左平行移动

个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则

.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年宁夏石嘴山市光明中学高三(上)期中数学试卷(理科)(解析版)
题型:填空题
已知下列命题:
①函数

的单调增区间是

.
②要得到函数

的图象,需把函数y=sinx的图象上所有点向左平行移动

个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则

.
其中正确命题的序号是
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知下列命题:
①函数
y=sin(-2x+)的单调增区间是
[-kπ-,-kπ+](k∈Z).
②要得到函数
y=cos(x-)的图象,需把函数y=sinx的图象上所有点向左平行移动
个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则
w≥π.
其中正确命题的序号是
②③④
②③④
.
查看答案和解析>>
科目:gzsx
来源:不详
题型:填空题
已知下列命题:
①函数
y=sin(-2x+)的单调增区间是
[-kπ-,-kπ+](k∈Z).
②要得到函数
y=cos(x-)的图象,需把函数y=sinx的图象上所有点向左平行移动
个单位长度.
③已知函数f(x)=2cos
2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则
w≥π.
其中正确命题的序号是______.
查看答案和解析>>
科目:gzsx
来源:
题型:
将函数y=
sin2x-cos2x的图象向右平移
个单位长度,所得图象对应的函数g(x)( )
| A、由最大值,最大值为+1 |
| B、对称轴方程是x=+kπ,k∈Z |
| C、是周期函数,周期T= |
| D、在区间[,]上单调递增 |
查看答案和解析>>
科目:gzsx
来源:
题型:
将函数y=2sin(
-2x)(x∈[0,π])向左平移
个单位长度,则平移后函数的单调递增区间是( )
查看答案和解析>>
科目:gzsx
来源:
题型:

已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=
的相关性质与图象.
(1)写出函数y=g(x)的定义域、值域及单调递增区间;
(2)作函数y=g(x)的大致图象(要充分反映由图象及条件给出的信息);
(3)试写出y=f(x)的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分).
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
17.

如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若g(x)的图象是将f(x)的图象向左平移$\frac{π}{3}$个单位长度得到的,求函数g(x)的单调递增区间;
(Ⅲ)设0<x<π,且h(x)=f(x)-m有两个不同的零点,求实数m的取值范围和这两个零点的和.
查看答案和解析>>
科目:gzsx
来源:江苏省淮安市四星级中学2008-2009学年度第一学期联考高一数学试卷苏教版 苏教版
题型:044
已知:函数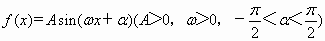 的最小正周期是π,且当
的最小正周期是π,且当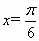 时f(x)取得最大值3.
时f(x)取得最大值3.
(1)求f(x)的解析式及单调增区间.
(2)若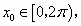 且
且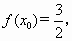 求x0
求x0
(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知:函数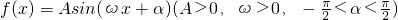 的最小正周期是π,且当
的最小正周期是π,且当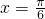 时f(x)取得最大值3.
时f(x)取得最大值3.
(1)求f(x)的解析式及单调增区间.
(2)若x0∈[0,2π),且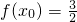 ,求x0.
,求x0.
(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年河南省周口市鹿邑三中高一(下)第三次月考数学试卷(理科)(解析版)
题型:解答题
已知:函数
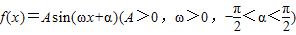
的最小正周期是π,且当
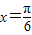
时f(x)取得最大值3.
(1)求f(x)的解析式及单调增区间.
(2)若x
∈[0,2π),且

,求x
.
(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:2013年湖南省怀化市高考数学二模试卷(理科)(解析版)
题型:选择题
如图展示了一个由区间(0,k)(其中k为一正实数)到实数集R上的映射过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB围成一个离心率为

的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
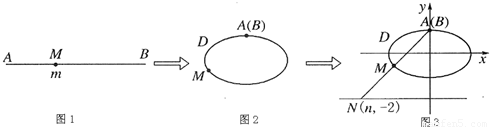
现给出下列5个命题①
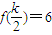
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
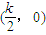
对称;⑤函数
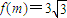
时AM过椭圆的右焦点.其中所有的真命题是( )
A.①③⑤
B.②③④
C.②③⑤
D.③④⑤
查看答案和解析>>
科目:gzsx
来源:
题型:
给出下列四个命题:
(1)“cosα=-
”是“α=2kπ+
,k∈Z”的必要不充分条件;
(2)终边在y轴上的角的集合是{a|a=
,k∈Z}.
(3)函数y=sin(2x-
)的一个单调增区间是[-
,
];
(4)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数的充要条件是f′(0)=0;
(5)为得到函数y=cos(2x+
)的图象,只需将函数y=sin2x的图象向左平移
个长度单位.
其中真命题的序号是
(把所有真命题的序号都填上).
查看答案和解析>>
科目:gzsx
来源:
题型:
有以下叙述:
①半径为1的圆中,60°的圆心角所对的弧的长度为
;
②已知函数f(x)=
(x≠±1),则f(2)+f(3)+f(4)+f(
)+f(
)+f(
)=3;
③函数y=-tan(2x-
)的单调递减区间是(
+
,
+
),k∈Z;
④设集合A=[0,
),B=[
,1],函数f(x)=
.若x0∈A,且f[f(x
0)]∈A,则x
0的取值范围是(
,
).
其中所有正确叙述的序号是
.
查看答案和解析>>

 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动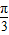 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是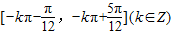 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=
已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)= 如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.
如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.![]() 的最小正周期是π,且当
的最小正周期是π,且当![]() 时f(x)取得最大值3.
时f(x)取得最大值3.![]() 且
且![]() 求x0
求x0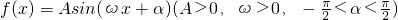 的最小正周期是π,且当
的最小正周期是π,且当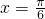 时f(x)取得最大值3.
时f(x)取得最大值3.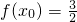 ,求x0.
,求x0.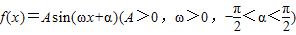 的最小正周期是π,且当
的最小正周期是π,且当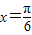 时f(x)取得最大值3.
时f(x)取得最大值3. ,求x.
,求x. 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
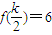 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点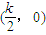 对称;⑤函数
对称;⑤函数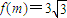 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )