如图.在三棱锥p-abq中答案解析

科目：gzsx 来源：2015届湖北省武汉市高三9月调考理科数学试卷（解析版） 题型：解答题

科目：gzsx 来源： 题型：

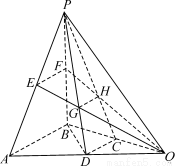
如图，在三棱锥P-ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连结GH．
（Ⅰ）求证：AB∥GH；
（Ⅱ）求平面PAB与平面PCD所成角的正弦值．

科目：gzsx 来源：2013年山东省高考数学试卷（理科）（解析版） 题型：解答题

如图所示，在三棱锥P-ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．
（1）求证：AB∥GH；
（2）求二面角D-GH-E的余弦值．

科目：gzsx 来源： 题型：解答题

8．如图，在三棱锥P-ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．
（1）证明：AB∥GH；
（2）求平面ABQ与平面EFQ所成二面角的正弦值．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：解答题

7．如图所示，在三棱锥P-ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．
（Ⅰ）求证：AB∥GH；
（Ⅱ）求异面直线DP与BQ所成的角；
（Ⅲ）求直线AQ与平面PDC所成角的正弦值．

科目：gzsx 来源： 题型：

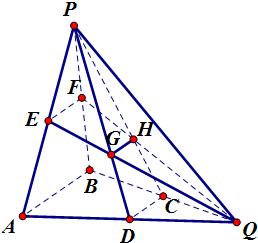（2013•山东）如图所示，在三棱锥P-ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．
（1）求证：AB∥GH；
（2）求二面角D-GH-E的余弦值．

科目：gzsx 来源： 题型：

如图，在三棱锥S-ABC中，设P、Q为底面△ABC内的两点，且

AP

=

2

5

AB

+

1

5

AC

，

AQ

=

2

3

AB

+

1

4

AC

，则V_S-ABP：V_S-ABQ=

4

5

4

5

．

科目：gzsx 来源：2013年普通高等学校招生全国统一考试(山东卷)、理科数学 题型：044

如图所示，在三棱锥P－ABQ中，PB⊥平面ABQ，BA＝BP＝BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ＝2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．

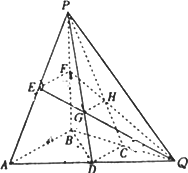
(Ⅰ)求证：AB∥GH；

(Ⅱ)求二面角D－GH－E的余弦值；

科目：gzsx 来源：2012-2013学年辽宁省铁岭市开原市高二（上）期末数学试卷（理科）（解析版） 题型：填空题

如图，在三棱锥S-ABC中，设P、Q为底面△ABC内的两点，且
=+，=，则V_S-ABP：V_S-ABQ=    ．

科目：gzsx 来源：不详 题型：填空题

如图，在三棱锥S-ABC中，设P、Q为底面△ABC内的两点，且

AP

=

2

5

AB

+

1

5

AC

，

AQ

=

2

3

AB

+

1

4

AC

，则V_S-ABP：V_S-ABQ=______．

科目：gzsx 来源： 题型：解答题

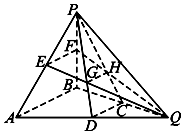12．如图所示，在三棱锥PABQ中，D，C，E，F分别是AQ，BQ，AP，BP的中点，PD与EQ交于点G，PC与FQ交于点H，连接GH．求证：
（1）求证：AB∥GH．
（2）若三棱锥P-ABQ为正四面体，且棱长为2，求多面体ADGE-BCHF的体积．