
科目:czsx 来源: 题型:
| a1,1 | a1,2 | a1,3 | a1,4 | a1,5 |
| a2,1 | a2,2 | a2,3 | a2,4 | a2,5 |
| a3,1 | a3,2 | a3,3 | a3,4 | a3,5 |
| a4,1 | a4,2 | a4,3 | a4,4 | a4,5 |
| a5,1 | a5,2 | a5,3 | a5,4 | a5,5 |
科目:gzsx 来源: 题型:
| n |  | i=1 |
科目:gzsx 来源: 题型:
| 2an |
| an+1 |
| 1 |
| an |
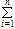 ai(ai-1)<3
ai(ai-1)<3 科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
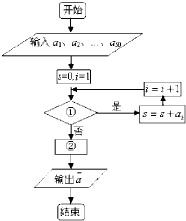 在阳光体育活动中,全校学生积极参加室外跑步,高三(1)班每个学生上个月跑步的路程从大到小排列依次是a1,a2,a3,…,a50(任意i=1,2,…,49,ai>ai+1),如图是计算该班上个月跑步路程前10名学生的平均路程的程序框图,则图中判断框①和处理框②内应分别填写( )
在阳光体育活动中,全校学生积极参加室外跑步,高三(1)班每个学生上个月跑步的路程从大到小排列依次是a1,a2,a3,…,a50(任意i=1,2,…,49,ai>ai+1),如图是计算该班上个月跑步路程前10名学生的平均路程的程序框图,则图中判断框①和处理框②内应分别填写( )A、i<10,
| ||||
B、i<11,
| ||||
C、i<11,
| ||||
D、i<10,
|
科目:gzsx 来源: 题型:
| n |
| ∑i=1 |
| 1 | ||||
|
| nP | ||||
|
科目:gzsx 来源: 题型:
| AB |
| AC |
| BD |
| DC |
| AI |
| BC |
| AC |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
 在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则科目:gzsx 来源: 题型:
 在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 1 |
| an |
| n |
 |
| i=1 |
科目:gzsx 来源: 题型:
| 2an |
| an+1 |
| n |
 |
| i=1 |
| 1 |
| a |
科目:gzsx 来源: 题型:
 在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,….则第3行第n个数为
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,….则第3行第n个数为