
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2016届浙江省杭州市九年级上学期第二次质检数学试卷(解析版) 题型:解答题
已知抛物线y1=ax2+bx+c的顶点坐标为( ,
,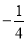 )且经过点A(1,0),直线y2=x+m恰好也经过点A
)且经过点A(1,0),直线y2=x+m恰好也经过点A
(1)分别求抛物线和直线的解析式;
(2)当x取何值时,函数值y2>y1;
(3)当0≤x≤2时,直接写出y2和y1的最小值分别为多少?
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
 如图,已知抛物线y1=ax2+bx+c的顶点坐标为(2,1),且经过点B(
如图,已知抛物线y1=ax2+bx+c的顶点坐标为(2,1),且经过点B(| 5 |
| 2 |
| 3 |
| 4 |
科目:czsx 来源:不详 题型:解答题
| 5 |
| 2 |
| 3 |
| 4 |
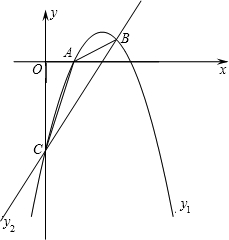
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
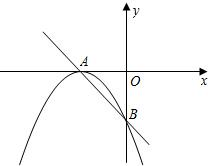 过点B.
过点B.科目:czsx 来源: 题型:解答题
 过点B.
过点B.科目:czsx 来源:2009-2010学年辽宁省大连市第55中学旅顺实验中学九年级(上)期中数学试卷(解析版) 题型:解答题
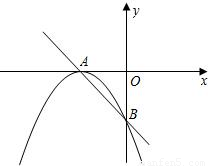
科目:czsx 来源: 题型:
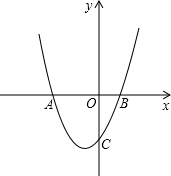 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;科目:czsx 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;科目:czsx 来源: 题型:解答题
科目:czsx 来源:不详 题型:解答题
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
科目:czsx 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
科目:czsx 来源: 题型:解答题
| x | … | -1 | 0 | 3 | … |
| y1=ax2+bx+c | … | 0 |  | 0 | … |
科目:czsx 来源: 题型:解答题
 已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.科目:czsx 来源: 题型:解答题
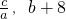 ),求当x≥1时y1的取值范围.
),求当x≥1时y1的取值范围.科目:czsx 来源: 题型:
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.
(1)求抛物线的解析式;
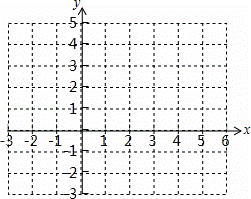
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
科目:czsx 来源:2013年初中毕业升学考试(贵州黔东南卷)数学(解析版) 题型:解答题
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.

(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
科目:czsx 来源:2013年天津市中考数学试卷 (解析版) 题型:解答题
| x | … | -1 | 3 | … | |
| y1=ax2+bx+c | … |  | … |