
科目:gzsx 来源:2007年普通高等学校招生全国统一考试理科数学卷(浙江) 题型:选择题
已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是准线上一点,且
是准线上一点,且 ,
, ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A. B.
B. C.
C. D.
D.
科目:gzsx 来源: 题型:
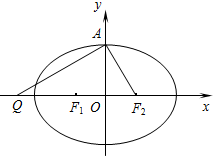 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 3 |
| MG |
| MH |
科目:gzsx 来源: 题型:
| F1F2 |
| F2Q |
| 0 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
| π |
| 3 |
| 3 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
科目:gzsx 来源: 题型:
 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
科目:gzsx 来源: 题型:
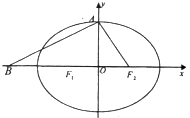 设椭圆D:
设椭圆D:| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
| 3 |
| OM |
| ON |
| OP |
科目:gzsx 来源: 题型:
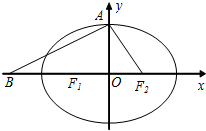 (2013•天津模拟)设椭圆C:
(2013•天津模拟)设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
| 3 |
科目:gzsx 来源: 题型:
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |