
科目:gzsx 来源: 题型:
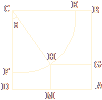
【例】某体育馆拟用运动场的边角地建一个矩形的健身室.如图所示,ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在![]() 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在![]() 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
科目:gzsx 来源:2015届广东省高一下学期期中考试数学试卷(解析版) 题型:解答题
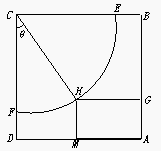
在申办国家级示范性高中期间,某校拟用运动场的边角地建一个矩形的健身室. 如图所示, 是一块边长为50m的正方形地皮,扇形
是一块边长为50m的正方形地皮,扇形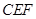 是运动场的一部分,其半径为40m,矩形
是运动场的一部分,其半径为40m,矩形 就是拟建的健身室,其中
就是拟建的健身室,其中
 分别在
分别在 和
和 上,
上, 在弧
在弧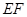 上,设矩形
上,设矩形 的面积为
的面积为 ,∠
,∠ .
.

(1) 试将 表示为
表示为 的函数;
的函数;
(2) 当点 在弧
在弧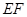 的何处时,该健身室的面积最大?最大面积为多少?
的何处时,该健身室的面积最大?最大面积为多少?
科目:gzsx 来源:2011年吉林省高一上学期期末质量检测数学试卷 题型:解答题
(本小题满分12分)
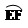
 某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
科目:gzsx 来源: 题型:

科目:gzsx 来源:学习高手必修五数学苏教版 苏教版 题型:044
一位技术员计划用下面的办法测试一种赛车:从时速10 km/h开始,每隔2 s速度提高20 km/h.如果测试时间是30 s,则测试距离是多长?
科目:gzsx 来源:2004年高考北京四中全真模拟试卷——数学 题型:044
某体育馆拟用运动场的边角地建一矩形的健身房,如图所示,ABCD是一块边长为50米的正方形地皮,扇形CEF是运动场的一部分,其半径为40米,矩形AGHM就是拟建的健身房,其中G、M分别在AB和AD上,H在![]() 上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在![]() 的何处时,该健身房的面积最大,最大面积是多少?
的何处时,该健身房的面积最大,最大面积是多少?

科目:gzsx 来源: 题型:
(本小题满分12分)
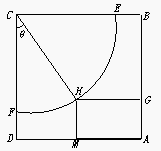
![]() 某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
科目:gzsx 来源: 题型:
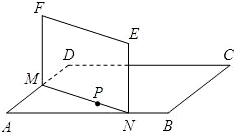 如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).科目:gzsx 来源: 题型:
| 76-x |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
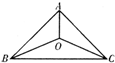 三个城市分别位于A,B,C三点处(如图),且AB=AC=20
三个城市分别位于A,B,C三点处(如图),且AB=AC=20| 2 |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
 如图,某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为xm,宽为ym.
如图,某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为xm,宽为ym.| 1 |
| x |
| 2 |
| y |
科目:gzsx 来源: 题型: