科目：gzsx 来源： 题型：

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N*，总有2S_n=a_n²+a_n．
（1）求数列{a_n}的通项公式；
（2）设正数数列{c_n}满足a_n+1=（c_n）ⁿ⁺¹，（n∈N^*），求数列{c_n}中的最大项；

查看答案和解析>>

科目：gzsx 来源： 题型：

已知各项均正的数列{a_n}的前n项和为S_n，且2S_n=

1

2

（a_n²+a_n）
（1）求{a_n}的通项公式
（2）设数列b_n=

1

anan+2

，求数列{b_n}的前n项的和T_n．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知{a_n}是正数组成的数列，其前n项和2S_n=a_n²+a_n（n∈N^*），数列{b_n}满足b1=

3

2

，bn+1=bn+3an(n∈N*)．
（I）求数列{a_n}，{b_n}的通项公式；
（II）若c_n=a_nb_n（n∈N^*），数列{c_n}的前n项和Tn，求

lim

n→∞

Tn

cn

．

查看答案和解析>>

科目：gzsx 来源： 题型：

设S_n是正项数列B的前n项和，2Sn=an2+an．
（Ⅰ）求证数列{a_n}是等差数列，并求{a_n}的通项公式；
（Ⅱ）已知bn=

an

2an

，求{b_n}的前n项和T_n．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知正数列{a_n}中的前n项和S_n满足2S_n=a_n²+a_n-2（n∈N^*）．
（1）求a₁，a₂，a₃的值，并求{a_n}的通项公式；
（2）设b_n=2ⁿ•a_n，求数列{b_n}的前n项和T_n；
（3）设cn=4n+(-1)n-1λ•2an（λ为非零整数，n∈N^*），试确定λ的值，使得对任意n∈N^*，有c_n+1＞c_n恒成立．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知数列{a_n}的各项均为正数，其前n项和为S_n，且满足2S_n=a_n²+a_n（n∈N^*）．
（Ⅰ）求a₁，a₂，a₃；
（Ⅱ）求数列{a_n}的通项公式；
（Ⅲ）若bn=n(

1

2

)an，求数列{b_n}的前n项和T_n．

查看答案和解析>>

科目：gzsx 来源： 题型：

设各项均为正数的数列{a_n}项和为S_n，且满足：2S_n=a_n²+a_n（n≥1，n∈N）．
（1）求a₁和a_n；
（2）设Tn=

1

S1

+

1

S2

+…+

1

Sn

，判断T_n与2的大小关系，并说明理由；
（3）设集合M=（m|m=2k，k∈N且1000≤k≤2011），若存在m₀∈M，使对满足n＞m₀的一切正整数n，不等式Sn＞

1

2

a

2

n

+1005恒成立，问这样的正整数m₀共有多少个？

查看答案和解析>>

科目：gzsx 来源： 题型：

（09年临沂高新区实验中学质检）（12分）

设数列{a_n}的各项都是正数，且对任意n∈N*,都有a₁³＋a₂³＋a₃³＋…＋a_n³＝S_n²，其中Sn为数例{a_n}的前n项和．

（1）求证：a_n²＝2S_n－a_n；

（2）求数列{a_n}的通项公式；

（3）设b_n＝3ⁿ＋（－1）ⁿ^－1λ・2a_n（λ为非零整数，n∈N*），试确定λ的值，使得对任意n∈N*,都有b_n_＋1>b_n成立．

查看答案和解析>>

科目：gzsx 来源：2011-2012学年河南省洛阳市高二（上）期末数学试卷（理科）（解析版） 题型：解答题

已知各项均正的数列{a_n}的前n项和为S_n，且2S_n=

（a_n²+a_n）
（1）求{a_n}的通项公式
（2）设数列b_n=

，求数列{b_n}的前n项的和T_n．

查看答案和解析>>

科目：gzsx 来源：黄州区模拟 题型：解答题

已知{a_n}是正数组成的数列，其前n项和2S_n=a_n²+a_n（n∈N^*），数列{b_n}满足b1=

3

2

，bn+1=bn+3an(n∈N*)．
（I）求数列{a_n}，{b_n}的通项公式；
（II）若c_n=a_nb_n（n∈N^*），数列{c_n}的前n项和Tn，求

lim

n→∞

Tn

cn

．

查看答案和解析>>

科目：gzsx 来源：山东省淄博市2011届高三第二次模拟数学理综试题 题型：044

设数列{a_n}的各项都是正数，且对任意n∈N^*，都有a₁³＋a₂3＋a₃³＋……＋a_n³＝s_n²，其中s_n为数列的前n项和．

(Ⅰ)求证：a_n²＝2s_n―a_n；

(Ⅱ)求数列{a_n}的通项公式；

(Ⅲ)设b_n＝3ⁿ＋(―1)^n－1λ·2^an(λ为非零整数，n∈N^*)，试确定l 的值，使得对任意的n∈N^*，都有b_n+1＞b_n成立．

查看答案和解析>>

科目：gzsx 来源： 题型：解答题

设各项均为正数的数列{a_n}项和为S_n，且满足：2S_n=a_n²+a_n（n≥1，n∈N）．
（1）求a₁和a_n；
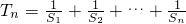（2）设 $数学公式$ ，判断T_n与2的大小关系，并说明理由；
（3）设集合M=（m|m=2k，k∈N且1000≤k≤2011），若存在m₀∈M，使对满足n＞m₀的一切正整数n，不等式 $数学公式$ 恒成立，问这样的正整数m₀共有多少个？

查看答案和解析>>

科目：gzsx 来源： 题型：解答题

已知正数列{a_n}中的前n项和S_n满足2S_n=a_n²+a_n-2（n∈N^）．
（1）求a₁，a₂，a₃的值，并求{a_n}的通项公式；
（2）设b_n=2ⁿ•a_n，求数列{b_n}的前n项和T_n；
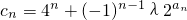（3）设 $数学公式$ （λ为非零整数，n∈N^），试确定λ的值，使得对任意n∈N^*，有c_n+1＞c_n恒成立．

查看答案和解析>>

科目：gzsx 来源：2010-2011学年福建省莆田四中高一（下）期末数学试卷（理科）（必修4、5）（解析版） 题型：解答题

已知正数列{a_n}中的前n项和S_n满足2S_n=a_n²+a_n-2（n∈N^*）．
（1）求a₁，a₂，a₃的值，并求{a_n}的通项公式；
（2）设b_n=2ⁿ•a_n，求数列{b_n}的前n项和T_n；
（3）设

（λ为非零整数，n∈N^*），试确定λ的值，使得对任意n∈N^*，有c_n+1＞c_n恒成立．

查看答案和解析>>

科目：gzsx 来源：2011-2012学年浙江省宁波市慈溪市高三（上）期中数学试卷（理科）（解析版） 题型：解答题

设各项均为正数的数列{a_n}项和为S_n，且满足：2S_n=a_n²+a_n（n≥1，n∈N）．
（1）求a₁和a_n；
（2）设

，判断T_n与2的大小关系，并说明理由；
（3）设集合M=（m|m=2k，k∈N且1000≤k≤2011），若存在m∈M，使对满足n＞m的一切正整数n，不等式

恒成立，问这样的正整数m共有多少个？

查看答案和解析>>

科目：gzsx 来源： 题型：解答题

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N，总有2S_n=a_n²+a_n．
（1）求数列{a_n}的通项公式；
（2）设正数数列{c_n}满足a_n+1=（c_n）ⁿ⁺¹，（n∈N^），求数列{c_n}中的最大项；

查看答案和解析>>

科目：gzsx 来源： 题型：解答题

已知{a_n}是正数组成的数列，其前n项和2S_n=a_n²+a_n（n∈N^），数列{b_n}满足 $数学公式$ ， $数学公式$ ．
（I）求数列{a_n}，{b_n}的通项公式；
（II）若c_n=a_nb_n（n∈N^），数列{c_n}的前n项和 $数学公式$ ．

查看答案和解析>>

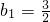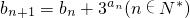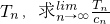科目：gzsx 来源：2010-2011学年甘肃省天水一中高三（上）第一次段考数学试卷（理科）（解析版） 题型：解答题

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N*，总有2S_n=a_n²+a_n．
（1）求数列{a_n}的通项公式；
（2）设正数数列{c_n}满足a_n+1=（c_n）ⁿ⁺¹，（n∈N^*），求数列{c_n}中的最大项；

查看答案和解析>>

科目：gzsx 来源：不详 题型：解答题

已知各项均正的数列{a_n}的前n项和为S_n，且2S_n=

1

2

（a_n²+a_n）
（1）求{a_n}的通项公式
（2）设数列b_n=

1

anan+2

，求数列{b_n}的前n项的和T_n．

查看答案和解析>>

科目：gzsx 来源：不详 题型：解答题

已知数列{a_n}的各项均为正数，其前n项和为S_n，且满足2S_n=a_n²+a_n（n∈N^*）．
（Ⅰ）求a₁，a₂，a₃；
（Ⅱ）求数列{a_n}的通项公式；
（Ⅲ）若bn=n(

1

2

)an，求数列{b_n}的前n项和T_n．

查看答案和解析>>

练习册

高中

初中

小学

an2+an=2Sn答案解析

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N，总有2S_n=a_n²+a_n．
（1）求数列{a_n}的通项公式；
（2）设正数数列{c_n}满足a_n+1=（c_n）ⁿ⁺¹，（n∈N^），求数列{c_n}中的最大项；

已知{a_n}是正数组成的数列，其前n项和2S_n=a_n²+a_n（n∈N^），数列{b_n}满足 $数学公式$ ， $数学公式$ ．
（I）求数列{a_n}，{b_n}的通项公式；
（II）若c_n=a_nb_n（n∈N^），数列{c_n}的前n项和 $数学公式$ ．

练习册

高中

初中

小学

an2+an=2Sn答案解析

已知正数列{an}中的前n项和Sn满足2Sn=an2+an-2（n∈N*）．（1）求a1，a2，a3的值，并求{an}的通项公式；（2）设bn=2n•an，求数列{bn}的前n项和Tn；（3）设（λ为非零整数，n∈N*），试确定λ的值，使得对任意n∈N*，有cn+1＞cn恒成立．

数列{an}的各项均为正数，Sn为其前n项和，对于任意n∈N*，总有2Sn=an2+an．（1）求数列{an}的通项公式；（2）设正数数列{cn}满足an+1=（cn）n+1，（n∈N*），求数列{cn}中的最大项；

已知{an}是正数组成的数列，其前n项和2Sn=an2+an（n∈N*），数列{bn}满足，．（I）求数列{an}，{bn}的通项公式；（II）若cn=anbn（n∈N*），数列{cn}的前n项和．

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N，总有2S_n=a_n²+a_n．
（1）求数列{a_n}的通项公式；
（2）设正数数列{c_n}满足a_n+1=（c_n）ⁿ⁺¹，（n∈N^），求数列{c_n}中的最大项；

已知{a_n}是正数组成的数列，其前n项和2S_n=a_n²+a_n（n∈N^），数列{b_n}满足 $数学公式$ ， $数学公式$ ．
（I）求数列{a_n}，{b_n}的通项公式；
（II）若c_n=a_nb_n（n∈N^），数列{c_n}的前n项和 $数学公式$ ．