
科目:gzsx 来源: 题型:
| 4 | 5 |
科目:gzsx 来源:2006年高考第一轮复习数学:9.11 多面体与正多面体(解析版) 题型:解答题

 .
.科目:gzsx 来源: 题型:
 已知:如图,矩形ABCD中点G为BC延长线上一点,连接DG,BH⊥DG于H,且GH=DH,点E,F分别在AB,BC上,且EF∥DG.
已知:如图,矩形ABCD中点G为BC延长线上一点,连接DG,BH⊥DG于H,且GH=DH,点E,F分别在AB,BC上,且EF∥DG.| 1 | 2 |
科目:gzsx 来源:2012-2013学年重庆94中高三(上)第五次月考数学试卷(解析版) 题型:解答题
 .
.
科目:gzsx 来源:湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型:047
已知:如图,α∥β,异面直线AB、CD和平面α、β分别交于A、B、C、D四点,E、F、G、H分别是AB、BC、CD、DA的中点,
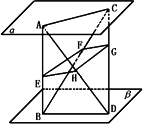
求证:(1)E、F、G、H共面;
(2)面EFGH∥平面α.
科目:gzsx 来源: 题型:
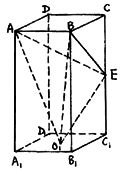
已知:如图,长方体ABCD—![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,E为
,E为![]() 的中点,
的中点,![]() 为下底面正方形的中心.求:(I)二面角C—AB—
为下底面正方形的中心.求:(I)二面角C—AB—![]() 的正切值;
的正切值;
(II)异面直线AB与![]() 所成角的正切值;
所成角的正切值;
(III)三棱锥![]() ——ABE的体积.
——ABE的体积.
 |
科目:gzsx 来源:2002年全国各省市高考模拟试题汇编 题型:044
已知:如图,长方体ABCD— 中,AB=BC=4,
中,AB=BC=4,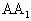 =8,E为
=8,E为 为下底面正方形的中心,求:
为下底面正方形的中心,求:
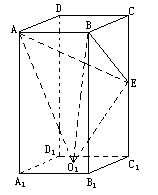
(Ⅰ)二面角C—AB— 的正切值:
的正切值:
(Ⅱ)异面直线AB与 所成角的正切值;
所成角的正切值;
(Ⅲ)三棱锥 —ABE的体积.
—ABE的体积.
科目:gzsx 来源:选修设计数学A4-1人教版 人教版 题型:047
圆内接四边形判定定理的推论的证明..
已知:如图,四边形ABCD,延长AB到E,∠EBC=∠CDA.

求证:A、B、C、D四点共圆.
科目:gzsx 来源:2014届山东省高二上学期期末模块调研理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知:如图,在四棱锥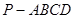 中,四边形
中,四边形 为正方形,
为正方形, ,且
,且 ,
,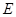 为
为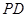 中点.
中点.
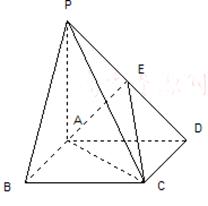
(1)证明: //平面
//平面 ;
;
(2)证明:平面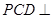 平面
平面 ;
;
(3)求二面角 的正弦值.
的正弦值.
科目:gzsx 来源:2012-2013学年甘肃省高三9月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知,如图,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交直线AC于点E,交AD于点F,过G作⊙O的切线,切点为H.

求证:(1)C,D,F,E四点共圆;
(2)GH2=GE·GF.
科目:gzsx 来源: 题型:
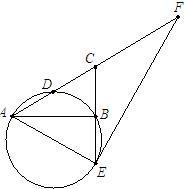 已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.
已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.科目:gzsx 来源: 题型:
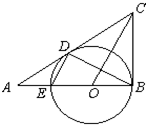 A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.| 1 |
| 1 |
| 1 |
| 1×2 |
| 1 |
| 1×2×3 |
| 1 |
| 1×2×3×L×n |
科目:gzsx 来源: 题型:
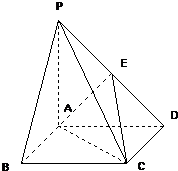 已知:如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=2,E为PD中点.
已知:如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=2,E为PD中点.科目:gzsx 来源: 题型:
 21、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
21、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.科目:gzsx 来源: 题型:
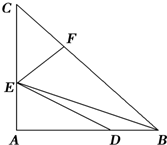 已知:如图,△ABC中,AB=AC,∠BAC=90°,AE=
已知:如图,△ABC中,AB=AC,∠BAC=90°,AE=| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
科目:gzsx 来源: 题型:
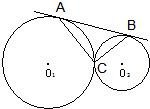 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=| 2 |
| R |
| r |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
科目:gzsx 来源: 题型:
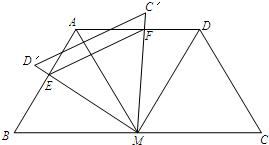 (2012•大丰市一模)已知:如图,M是线段BC的中点,BC=4,分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD,连接AD.
(2012•大丰市一模)已知:如图,M是线段BC的中点,BC=4,分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD,连接AD.科目:gzsx 来源: 题型:
 (2013•济南一模)已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=
(2013•济南一模)已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=| 1 | 2 |