科目:czsx 来源: 题型:022
(2005湖北武汉)如图所示平面直角坐标系中,点A、B、C的坐标分别是A(-2,5),B(-3,-1),C(1,-1),在第一象限内找一点D,使四边形ABCD是平行四边形,那么点D的坐标是(____,____).
科目:czsx 来源: 题型:
| 5 |
| 5 |
科目:czsx 来源: 题型:
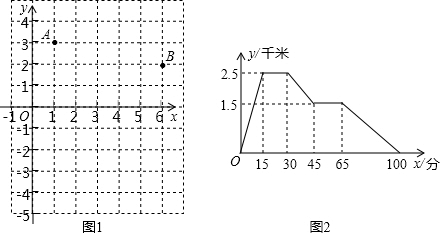
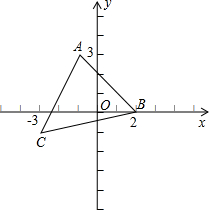 如图已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)
如图已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)科目:czsx 来源: 题型:
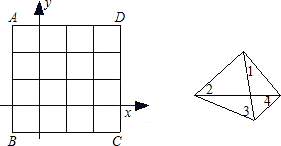 方形面上的概率为
方形面上的概率为| 1 | 4 |
科目:czsx 来源: 题型:
| 3 |
科目:czsx 来源: 题型:
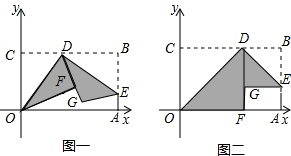 如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.
如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.| 1 |
| 24 |
| 1 |
| 24 |
科目:czsx 来源: 题型:
| 1 |
| 2 |
| 12 |
| 5 |

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
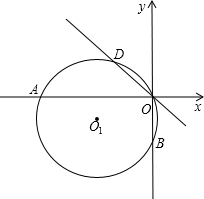
| 7 | 2 |
科目:czsx 来源: 题型:
| 4 |
| t |
| 4 |
| t |
| 1 |
| 4 |
| 1 |
| 4 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 3 |
| 70 |
| 3 |
| 70 |
科目:czsx 来源: 题型:
| 3 |

科目:czsx 来源: 题型:
| 3 |
| 5 |
 角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=| k |
| x |
科目:czsx 来源:2013届北京市西城区(北区)九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图1,平面直角坐标系中,抛物线 与
与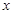 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
(1)若点F的坐标为( ,
, ),AF=
),AF= .
.
①求此抛物线的解析式;
②点P是此抛物线上一个动点,点Q在此抛物线的对称轴上,以点A、F、P、Q为顶点构成的四边形是平行四边形,请直接写出点Q的坐标;
(2)若 ,
,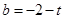 ,且AB的长为
,且AB的长为 ,其中
,其中 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求 的值和∠DFA的正切值.
的值和∠DFA的正切值.
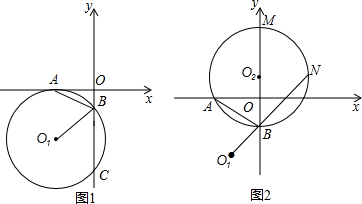
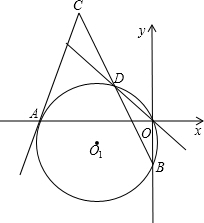
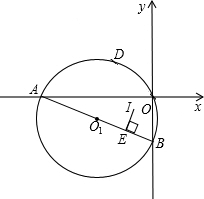
科目:czsx 来源:2008-2009学年湖北省武汉市江岸区九年级(上)期中数学试卷(解析版) 题型:解答题


 ,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O1的大小发生变化时,其结论:AE-BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围.
,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O1的大小发生变化时,其结论:AE-BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围.
科目:czsx 来源:2012届江苏省南京市溧水县中考一模数学试卷(带解析) 题型:解答题
七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
|
|
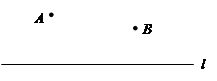
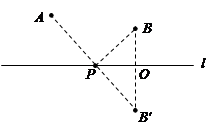 我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
科目:czsx 来源:2013年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系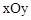 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,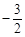 ),点M是抛物线C2:
),点M是抛物线C2: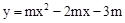 (
(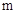 <0)的顶点.
<0)的顶点.
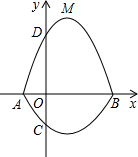
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
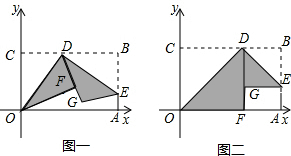
(3)当△BDM为直角三角形时,求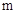 的值.
的值.
科目:czsx 来源: 题型:解答题
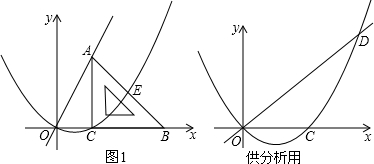
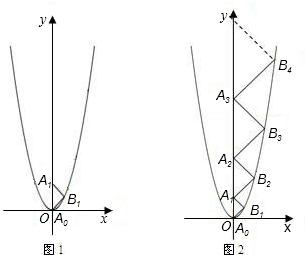
 如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.
如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.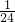 x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-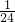 x2+6始终有公共点,请在图一中作出这样的公共点.
x2+6始终有公共点,请在图一中作出这样的公共点.科目:czsx 来源: 题型:解答题