科目:czsx 来源: 题型:
 如图,抛物线:y=
如图,抛物线:y=| 1 | 2 |
科目:czsx 来源:2011-2012学年江苏如城新民初中九年级上期末考试数学试卷(解析版) 题型:解答题
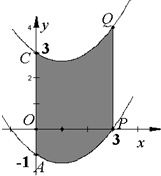
如图,抛物线y= x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).
x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).
(1)求抛物线的解析式;
(2)点Q是线段OB上的动点,过点Q作QE//BC,交AC于点E,连接CQ,设OQ=m,当△CQE的面积最大时,求m的值,并写出点Q的坐标.
(3)若平行于x轴的动直线,与该抛物线交于点P,与直线BC交于点F,D的坐标为(-2,0),则是否存在这样的直线l,使OD=DF?若存在,求出点P的坐标;若不存在,请说明理由.
科目:czsx 来源:2012届江苏省无锡锡山区九年级下学期期中考试数学卷(解析版) 题型:解答题
如图,抛物线y= +bx+c的顶点为C(0,-
+bx+c的顶点为C(0,- ),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒
),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒 个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.
个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.

(1)求二次函数的解析式;
(2)设△TSC的面积为S,求S关于t的函数解析式;
(3)以点T为圆心,TB为半径的圆与射线BC交于点E,试说明:在点T运动的过程中,线段ED的长是一定值,并求出该定值.
科目:czsx 来源:2011-2012学年江苏省无锡锡山区九年级下学期期中考试数学卷(带解析) 题型:解答题
如图,抛物线y= +bx+c的顶点为C(0,-
+bx+c的顶点为C(0,- ),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒
),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒 个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.
个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.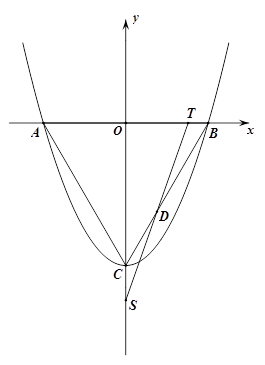
(1)求二次函数的解析式;
(2)设△TSC的面积为S,求S关于t的函数解析式;
(3)以点T为圆心,TB为半径的圆与射线BC交于点E,试说明:在点T运动的过程中,线段ED的长是一定值,并求出该定值.
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
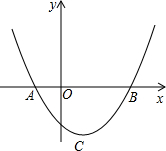
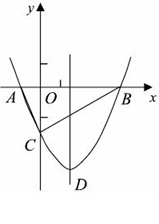
如图,抛物线y= y=![]() x2 + bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2 + bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
 |
科目:czsx 来源:2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型:解答题
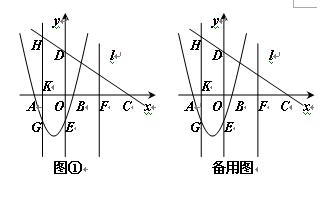
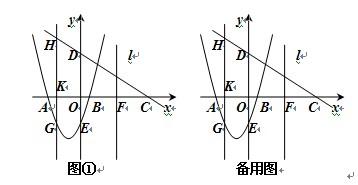
(本题12分)如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3)。点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行。直线y=-x+m过点C,交y轴于D点.
⑴求抛物线的函数表达式;
⑵点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于 点G,求线段HG长度的最大值;
⑶在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
科目:czsx 来源:2012年初中毕业升学考试(黑龙江龙东地区卷)数学(解析版) 题型:解答题
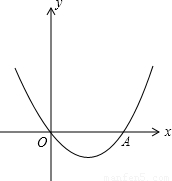
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0)。
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且 ,求点B的坐标。
,求点B的坐标。
科目:czsx 来源:2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型:解答题
(本题12分) 如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3)。点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行。直线y=-x+m过点C,交y轴于D点.
⑴求抛物线的函数表达式;
⑵点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于 点G,求线段HG长度的最大值;
⑶在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.

科目:czsx 来源: 题型:
(本题12分) 如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3)。点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行。直线y=-x+m过点C,交y轴于D点.
⑴求抛物线的函数表达式;
⑵点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于 点G,求线段HG长度的最大值;
⑶在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.

科目:czsx 来源:2012年初中毕业升学考试(黑龙江龙东地区卷)数学(带解析) 题型:解答题
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0)。
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且 ,求点B的坐标。
,求点B的坐标。
科目:czsx 来源: 题型:
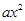 +bx+c的顶点为C(0,-
+bx+c的顶点为C(0,-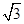 ),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒
),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒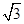 个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.
个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.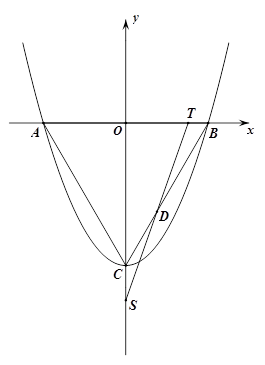
科目:czsx 来源: 题型:
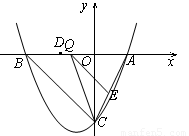
如图,抛物线y=![]() +bx+c的顶点为C(0,-
+bx+c的顶点为C(0,-![]() ),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒
),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒![]() 个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.
个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.

(1)求二次函数的解析式;
(2)设△TSC的面积为S,求S关于t的函数解析式;
(3)以点T为圆心,TB为半径的圆与射线BC交于点E,试说明:在点T运动的过程中,线段ED的长是一定值,并求出该定值.
科目:czsx 来源:2011-2012学年江苏如城新民初中九年级上期末考试数学试卷(带解析) 题型:解答题
如图,抛物线y=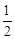 x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).
x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).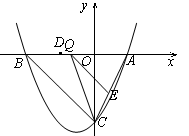
(1)求抛物线的解析式;
(2)点Q是线段OB上的动点,过点Q作QE//BC,交AC于点E,连接CQ,设OQ=m,当△CQE的面积最大时,求m的值,并写出点Q的坐标.
(3)若平行于x轴的动直线,与该抛物线交于点P,与直线BC交于点F,D的坐标为(-2,0),则是否存在这样的直线l,使OD=DF?若存在,求出点P的坐标;若不存在,请说明理由.
科目:czsx 来源:江苏期末题 题型:解答题
如图,抛物线经y=-x2+bx+c过点A(1,0),点B(0,-4),

科目:czsx 来源: 题型:单选题
科目:czsx 来源: 题型:
如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3)。点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行。直线y=-x+m过点C,交y轴于D点。
⑴求抛物线的函数表达式;
⑵点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
⑶在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标。
科目:czsx 来源: 题型:
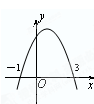
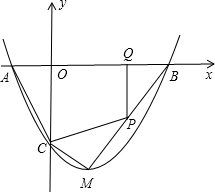 如图,抛物线y=ax2+bx+c与x轴交于A、B两点的横坐标分别是-1,3 (点A在点B左侧),与y轴交于点C,抛物线的顶点M在直线y=3x-7上.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点的横坐标分别是-1,3 (点A在点B左侧),与y轴交于点C,抛物线的顶点M在直线y=3x-7上.科目:czsx 来源: 题型:
 (2013•思明区一模)如图,抛物线y=ax2-bx+c(a>1)过点A(1,0),且对称轴为x=2,直线y=kx+m(k>0)与抛物线交于点A和点B.
(2013•思明区一模)如图,抛物线y=ax2-bx+c(a>1)过点A(1,0),且对称轴为x=2,直线y=kx+m(k>0)与抛物线交于点A和点B.科目:czsx 来源: 题型: