练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知函数y=-ax2+bx+c(a≠0)图象过点P(-1，2)和Q(2，4). (1)证明：无论a为任何实数时，抛物线的图象与X轴的交点在原点两侧

    已知函数y=-ax2+bx+c(a≠0)图象过点P(-1，2)和Q(2，4). (1)证明：无论a为任何实数时，抛物线的图象与X轴的交点在原点两侧答案解析

    科目：czsx 来源： 题型：

    已知函数y=kx,且k<0,图象过点(-1,y1)、(-2,y2),则y1与y2的大小关系为

    A.y1=y2                                  B.y1<y2

    C.y1>y2                                  D.无法确定

    查看答案和解析>>

    科目：czsx 来源：数学课外练习八年级下学期使用 题型：013

    已知函数y＝3x＋k的图象过点(1，2)，则函数y＝kx＋2的图象大致为图中的

    [　　]

    A．

    B．

    C．

    D．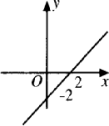

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知函数y=kx,且k<0,图象过点(-1,y1)、(-2,y2),则y1与y2的大小关系为

    A.y1=y2           B.y1<y2    C.y1>y2          D.无法确定

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知函数y=kx,且k<0,图象过点(-1,y1)、(-2,y2),则y1与y2的大小关系为

    A.y1=y2                                  B.y1<y2

    C.y1>y2                                  D.无法确定

    查看答案和解析>>

    科目：czsx 来源： 题型：

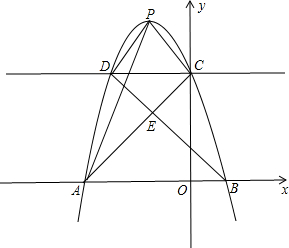
    （2012•瑶海区三模）已知抛物线y=ax2+bx+c（a≠0）过点A（-3，0），B（1，0），C（0，3）三点．
    （1）求该抛物线的函数关系式；
    （2）若抛物线的顶点为P，连接PA、AC、CP，求△PAC的面积；
    （3）过点C作y轴的垂线，交抛物线于点D，连接PD、BD，BD交AC于点E，判断四边形PCED的形状，并说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

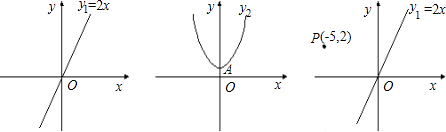
    已知一次函数y1=2x，二次函数y2=mx2-3（m-1）x+2m-1的图象关于y轴对称，y2的顶点为A．
    （1）求二次函数y2的解析式；
    （2）将y2左右平移得到y3交y2于P点，过P点作直线l∥x轴交y3于点M，若△PAM为等腰三角形，求P点坐标；
    （3）是否存在二次函数y4=ax2+bx+c，其图象经过点（-5，2），且对于任意一个实数x，这三个函数所对应的函数值y1、y2、y4都有y1≤y4≤y2成立？若存在，求出函数y4的解析式；若不存在，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，已知抛物线y=ax2+bx+c（a≠0）过点A（3，0），B（1，0），且与y轴交于点C（0，-3），精英家教网点P是抛物线AC间上一动点，从点C沿抛物线向点A运动（点P与A、C不重合），过点P作PD∥y轴，交AC于点D．
    （1）求该抛物线的函数关系式；
    （2）当△ADP是直角三角形时，直接写出点P的坐标；
    （3）求线段PD的最大值，并求最大值时P点的坐标；
    （4）在问题（3）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x -3 -2 -1 0 1 2 3
    y1=2x              
    y2=x2+1              
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2012年安徽省合肥市瑶海区中考数学三模试卷（解析版） 题型：解答题

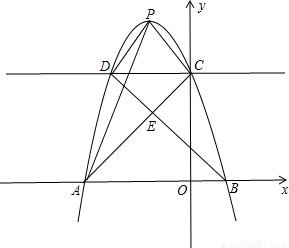
    已知抛物线y=ax2+bx+c（a≠0）过点A（-3，0），B（1，0），C（0，3）三点．
    （1）求该抛物线的函数关系式；
    （2）若抛物线的顶点为P，连接PA、AC、CP，求△PAC的面积；
    （3）过点C作y轴的垂线，交抛物线于点D，连接PD、BD，BD交AC于点E，判断四边形PCED的形状，并说明理由．

    查看答案和解析>>

    科目：czsx 来源：2007年广东省广州市越秀区中考数学二模试卷（解析版） 题型：解答题

    已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x-3-2-1123
    y1=2x       
    y2=x2+1       
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知一次函数y1=2x，二次函数y2=mx2-3（m-1）x+2m-1的图象关于y轴对称，y2的顶点为A．
    （1）求二次函数y2的解析式；
    （2）将y2左右平移得到y3交y2于P点，过P点作直线l∥x轴交y3于点M，若△PAM为等腰三角形，求P点坐标；
    （3）是否存在二次函数y4=ax2+bx+c，其图象经过点（-5，2），且对于任意一个实数x，这三个函数所对应的函数值y1、y2、y4都有y1≤y4≤y2成立？若存在，求出函数y4的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2006年江苏省淮安市淮阴中学高一分班考试数学试卷（解析版） 题型：解答题

    已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x-3-2-1123
    y1=2x       
    y2=x2+1       
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2004年天津市中考数学试卷（解析版） 题型：解答题

    （2004•天津）已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x-3-2-1123
    y1=2x       
    y2=x2+1       
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2012年江苏省泰州市泰兴市济川中学中考数学一模试卷（解析版） 题型：解答题

    已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x-3-2-1123
    y1=2x       
    y2=x2+1       
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2012年广东省深圳市中考数学全真模拟试卷（五）（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+c（a≠0）过点A（3，0），B（1，0），且与y轴交于点C（0，-3），点P是抛物线AC间上一动点，从点C沿抛物线向点A运动（点P与A、C不重合），过点P作PD∥y轴，交AC于点D．
    （1）求该抛物线的函数关系式；
    （2）当△ADP是直角三角形时，直接写出点P的坐标；
    （3）求线段PD的最大值，并求最大值时P点的坐标；
    （4）在问题（3）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2012年江苏省南京市雨花台区中考数学一模试卷（解析版） 题型：解答题

    已知抛物线y=ax2+bx+c（a≠0）过点A（-3，0），B（1，0），C（0，3）三点．
    （1）求该抛物线的函数关系式；
    （2）若抛物线的顶点为P，连接PA、AC、CP，求△PAC的面积；
    （3）过点C作y轴的垂线，交抛物线于点D，连接PD、BD，BD交AC于点E，判断四边形PCED的形状，并说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011年湖北省武汉市黄陂区九年级部分学校联考数学试卷（解析版） 题型：解答题

    已知一次函数y1=2x，二次函数y2=mx2-3（m-1）x+2m-1的图象关于y轴对称，y2的顶点为A．
    （1）求二次函数y2的解析式；
    （2）将y2左右平移得到y3交y2于P点，过P点作直线l∥x轴交y3于点M，若△PAM为等腰三角形，求P点坐标；
    （3）是否存在二次函数y4=ax2+bx+c，其图象经过点（-5，2），且对于任意一个实数x，这三个函数所对应的函数值y1、y2、y4都有y1≤y4≤y2成立？若存在，求出函数y4的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011年广东省深圳市中考数学全真模拟试卷（二）（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+c（a≠0）过点A（3，0），B（1，0），且与y轴交于点C（0，-3），点P是抛物线AC间上一动点，从点C沿抛物线向点A运动（点P与A、C不重合），过点P作PD∥y轴，交AC于点D．
    （1）求该抛物线的函数关系式；
    （2）当△ADP是直角三角形时，直接写出点P的坐标；
    （3）求线段PD的最大值，并求最大值时P点的坐标；
    （4）在问题（3）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x-3-2-10123
    y1=2x
    y2=x2+1
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2004年全国中考数学试题汇编《二次函数》（05）（解析版） 题型：解答题

    （2004•天津）已知一次函数y1=2x，二次函数y2=x2+1．
    （Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
    x-3-2-1123
    y1=2x       
    y2=x2+1       
    （Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
    （Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．

    查看答案和解析>>