精英家教网 >
试题搜索列表 >若两个不等实数,m,n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是
若两个不等实数,m,n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是答案解析
科目:czsx
来源:
题型:
(2013•黔东南州)若两个不等实数m、n满足条件:m
2-2m-1=0,n
2-2n-1=0,则m
2+n
2的值是
6
6
.
查看答案和解析>>
科目:czsx
来源:
题型:
若两个不等实数m、n满足条件:m
2-2m-1=0,n
2-2n-1=0,则m+n的值是
2
2
.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(贵州黔东南卷)数学(解析版)
题型:填空题
若两个不等实数m、n满足条件:m2﹣2m﹣1=0,n2﹣2n﹣1=0,则m2+n2的值是 .
查看答案和解析>>
科目:czsx
来源:2013年贵州省黔东南高级中等学校招生考试数学
题型:022
若两个不等实数m、n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是________.
查看答案和解析>>
科目:czsx
来源:黔东南州
题型:填空题
若两个不等实数m、n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是______.
查看答案和解析>>
科目:czsx
来源:
题型:
若两个不等实数m、n满足条件:m2﹣2m﹣1=0,n2﹣2n﹣1=0,则m2+n2的值是 6 .
查看答案和解析>>
科目:czsx
来源:2013年贵州省黔东南州中考数学试卷(解析版)
题型:填空题
若两个不等实数m、n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是 .
查看答案和解析>>
科目:czsx
来源:
题型:填空题
若两个不等实数m、n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是________.
查看答案和解析>>
科目:czsx
来源:
题型:
关于x的一元二次方程(a-5)x2-4x-1=0有两个不等实数根,则a满足( )
A. a≥ 1 B.a≥1且a≠ 5 C. a>1且a≠ 5 D.a≠5
a>1且a≠ 5 D.a≠5
查看答案和解析>>
科目:czsx
来源:
题型:
关于x的一元二次方程(a-5)x2-4x-1=0有两个不等实数根,则a满足( )
A. a≥ 1 B.a≥1且a≠ 5 C. a>1且a≠ 5 D.a≠5
a>1且a≠ 5 D.a≠5
查看答案和解析>>
科目:czsx
来源:
题型:
已知下列命题:①同位角相等;②若ac<0,则方程cx2+bx+a=0有两个不等实数根;③对角线相等且互相垂直的四边形是正方形;④抛物线y=x2-2x与坐标轴有3个不同交点;⑤边长相等的多边形内角都相等.从中任选一个命题是真命题的概率为( )
查看答案和解析>>
科目:czsx
来源:
题型:
下列命题:
①若b=2a+
c,则一元二次方程ax
2+bx+c=O必有一根为-2;
②若ac<0,则方程cx
2+bx+a=O有两个不等实数根;
③若b
2-4ac=0,则方程cx
2+bx+a=O有两个相等实数根;
其中正确的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:
11、对于一元二次方程ax2+bx+c=O(a≠0),下列说法:
①若a+c=0,方程ax2+bx+c=O必有实数根;
②若b2+4ac<0,则方程ax2+bx+c=O一定有实数根;
③若a-b+c=0,则方程ax2+bx+c=O一定有两个不等实数根;
④若方程ax2+bx+c=O有两个实数根,则方程cx2+bx+a=0一定有两个实数根.
其中正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
所谓配方法其实就是逆用完全平方公式,即a
2±2ab+b
2=(a±b)
2.该方法在数、式、方程等多方面应用非常广泛,如3+2
=12+2
+(
)
2;x
2+2x+5=x
2+2x+1+4=(x+1)
2+4等等.请你用配方法解决以下问题:
(1)解方程:x
2=5+2
;(不能出现形如
的双重二次根式)
(2)若a
2+4b
2+c
2-2a-8b+10c+30=0,解关于x的一元二次方程ax
2-bx+c=0;
(3)求证:不论m为何值,解关于x的一元二次方程x
2+(m-1)x+m-3=0总有两个不等实数根.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•长沙)设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=
是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数y=
x
2-
x-
是闭区间[a,b]上的“闭函数”,求实数a,b的值.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•如东县模拟)若两圆的半径r1,r2是方程x2-4x+3=0的两个不等实数根,圆心距为5,则两圆的位置关系为( )
查看答案和解析>>
科目:czsx
来源:
题型:
已知关于x的方程mx2-(3m+2)x+2m+2=0
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若关于x的方程mx2-(3m+2)x+2m+2=0的两个不等实数根均为正整数,且m为整数,求m的值.
查看答案和解析>>
科目:czsx
来源:
题型:
所谓配方法其实就是逆用完全平方公式,即a
2±2ab+b
2=(a+b)
2.该方法在数、式、方程等多方面应用非常广泛,如
3+2
=1
2+2
+(
)
2=(1+
)
2;x
2+2x+5=x
2+2x+1+4=(x+1)
2+4等等.请你用配方法解决以下问题:
(1)解方程:x
2=5+2
;(不能出现形如
的双重二次根式)
(2)求证:不论m为何值,解关于x的一元二次方程x
2+(m-1)x+m-3=0总有两个不等实数根.
(3)若a
2+4b
2+c
2-2a-8b+10c+30=0,解关于x的一元二次方程ax
2-bx+c=0.
查看答案和解析>>
科目:czsx
来源:
题型:
所谓配方法其实就是逆用完全平方公式,即

.该方法在数、式、方程等多方面应用非常广泛,如
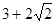

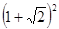
;
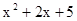
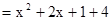
=
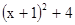
等等.请你用配方法解决以下问题:
【小题1】解方程:
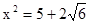
;(不能出现形如
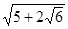
的双重二次根式)
【小题2】)若
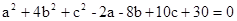
,解关于x的一元二次方程
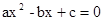
;
【小题3】求证:不论m为何值,解关于x的一元二次方程
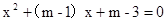
总有两个不等实数根
查看答案和解析>>
科目:czsx
来源:2013年湖南省长沙市中考数学试卷(解析版)
题型:解答题
设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=

是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数y=

x
2-

x-

是闭区间[a,b]上的“闭函数”,求实数a,b的值.
查看答案和解析>>

![]() a>1且a≠ 5 D.a≠5
a>1且a≠ 5 D.a≠5![]() a>1且a≠ 5 D.a≠5
a>1且a≠ 5 D.a≠5 .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如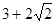

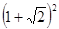 ;
;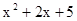
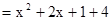 =
=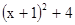 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题: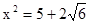 ;(不能出现形如
;(不能出现形如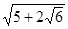 的双重二次根式)
的双重二次根式)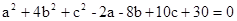 ,解关于x的一元二次方程
,解关于x的一元二次方程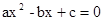 ;
;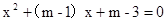 总有两个不等实数根
总有两个不等实数根  是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由; x2-
x2- x-
x- 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.