科目：gzsx 来源： 题型：
| a(x-1)2+1 |
| bx+c-b |
| e |
科目：gzsx 来源： 题型：
设a≥0，f (x)=x－1－ln2 x＋2a ln x（x>0）.
（Ⅰ）令F（x）＝xf＇（x），讨论F（x）在（0.＋
）内的单调性并求极值；
（Ⅱ）求证：当x>1时，恒有x>ln2x－2a ln x＋1.
科目：gzsx 来源：广东省普宁市09-10学年高二下学期期末考试数学试题 题型：解答题
设a≥0，f (x)=x－1－ln2 x＋2a ln x（x>0）.
（1）令F（x）＝xf＇（x），讨论F（x）在（0.＋∞）内的单调性并求极值；
（2）求证：当x>1时，恒有x>ln2x－2a ln x＋1.
科目：gzsx 来源：不详 题型：解答题
| a(x-1)2+1 |
| bx+c-b |
| e |
科目：gzsx 来源： 题型：
（07年安徽卷理）(本小题满分14分)
设a≥0，f (x)=x－1－ln2 x＋2a ln x（x>0）.
（Ⅰ）令F（x）＝xf＇（x），讨论F（x）在（0.＋∞）内的单调性并求极值；
（Ⅱ）求证：当x>1时，恒有x>ln2x－2a ln x＋1.
科目：gzsx 来源： 题型：解答题
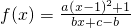（a，b，c∈N），且f（2）=2，f（3）＜3，
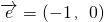平移后得到的图象关于原点对称．科目：gzsx 来源：2014届内蒙古呼伦贝尔市高二上期中考理科数学试卷（解析版） 题型：选择题
不等式｜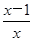
｜>1的解集是
A．{x｜x>1}
B．{x｜x<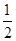
}
C．{x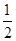｜<x<1}
D．{x｜x<0，或0<x< }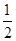
科目：gzsx 来源：2013届贵州省高二期中考试理科数学试卷（解析版） 题型：解答题
已知函数f(x)＝
x2＋lnx.
(1)求函数f(x)的单调区间；
(2)求证：当x>1时，x2＋lnx<
x3.
科目：gzsx 来源：2011年四川省内江六中高考数学模拟试卷（文科）（解析版） 题型：解答题
（a，b，c∈N），且f（2）=2，f（3）＜3，
平移后得到的图象关于原点对称．科目：gzsx 来源：2008-2009学年年重庆市部分重点中学高三（上）12月月考数学试卷（理科）（解析版） 题型：解答题
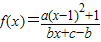（a，b，c∈N），且f（2）=2，f（3）＜3，
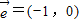平移后得到的图象关于原点对称．科目：gzsx 来源：2011年江西省抚州市临川二中高考数学一模试卷（文科）（解析版） 题型：解答题
科目：gzsx 来源：江西省重点中学盟校2010届高三第二次联考理科试题 题型：解答题
（本小题满分12
分）
设函数f(x)的定义域为R，若|f(x)|≤|x|对任意的实数x均成立，则称函数f(x)为
函数。
（1）试判断函数
=
=
中哪些是函数，并说明理由；
（2）求证：若a>1，则函数f(x)=ln(x2+a)-lna是函数。
科目：gzsx 来源： 题型：
（08年舞阳一高四模理）（12分） 设a≥0，f (x)=x－1－ln2 x＋2a ln x（x>0）.
（Ⅰ）令F（x）＝xf＇（x），讨论F（x）在（0.＋∞）内的单调性并求极值；
（Ⅱ）求证：当x>1时，恒有x>ln2x－2a ln x＋1.
科目：gzsx 来源：2007年普通高等学校招生全国统一考试理科数学卷（安徽） 题型：解答题
(本小题满分14分)
设a≥0，f (x)=x－1－ln2 x＋2a ln x（x>0）.
（Ⅰ）令F（x）＝xf＇（x），讨论F（x）在（0.＋∞）内的单调性并求极值；
（Ⅱ）求证：当x>1时，恒有x>ln2x－2a ln x＋1.
科目：gzsx 来源： 题型：
.设a≥0，f (x)=x－1－ln2 x＋2a ln x（x>0）.
（Ⅰ）令F（x）＝xf＇（x），讨论F（x）在（0.＋∞）内的单调性并求极值；
（Ⅱ）求证：当x>1时，恒有x>ln2x－2a ln x＋1.
科目：gzsx 来源：安徽省高考真题 题型：解答题
时，求证tanx＞x+
;
x2.