
科目:czsx 来源: 题型:单选题
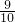
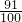

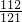
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| a |
| A、1 | B、0 | C、3 | D、4 |
科目:czsx 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| A、1 | B、2 | C、3 | D、4 |
科目:czsx 来源: 题型:
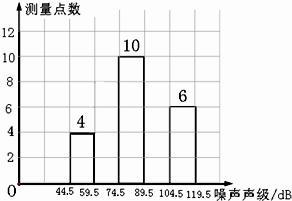
| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
科目:czsx 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 3 |
科目:czsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
科目:czsx 来源: 题型:
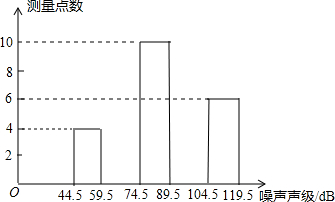 行处理(设所测数据是正整数),得频数分布表如下:
行处理(设所测数据是正整数),得频数分布表如下:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5--119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
科目:czsx 来源: 题型:
| p |
| q |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| a |
| A、1个 | B、2个 | C、3个 | D、4个 |
科目:czsx 来源: 题型:
| A、16 | B、10 | C、4 | D、1 |
科目:czsx 来源: 题型:
| P |
| q |
| 4 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
科目:czsx 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| n |
科目:czsx 来源: 题型: