
科目:czsx 来源: 题型:
 如图所示,在长和宽分别是a,b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a,b的矩形纸片的四个角都剪去一个边长为x的正方形.科目:czsx 来源: 题型:
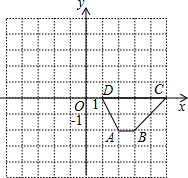 -2),C(5,0),D(1,0),将梯形ABCD绕点D逆时针旋转90°得到梯形A1B1C1D.
-2),C(5,0),D(1,0),将梯形ABCD绕点D逆时针旋转90°得到梯形A1B1C1D.科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
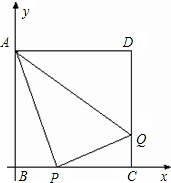 如图所示,在平面直角坐标系中,正方形ABCD的边长为4,点B在原点上,P是BC上一动点,QP⊥AP交DC于Q,设PB=x,△ADQ的面积为y.
如图所示,在平面直角坐标系中,正方形ABCD的边长为4,点B在原点上,P是BC上一动点,QP⊥AP交DC于Q,设PB=x,△ADQ的面积为y.| 2 | 3 |
科目:czsx 来源: 题型:
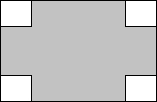 如图所示,在长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形,折叠后,做成一个无盖的盒子(单位:cm)
如图所示,在长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形,折叠后,做成一个无盖的盒子(单位:cm)科目:czsx 来源: 题型:
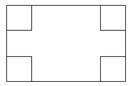 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形后做成一个无盖的盒子.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形后做成一个无盖的盒子. 科目:czsx 来源: 题型:
| 3 | 4 |
 在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.科目:czsx 来源: 题型:
 25、如图所示,在长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm)
25、如图所示,在长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm)科目:czsx 来源: 题型:
 22、如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.
22、如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.科目:czsx 来源: 题型:
 如图所示,在长和宽分别是a与b的长方形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a与b的长方形纸片的四个角都剪去一个边长为x的正方形.科目:czsx 来源: 题型:
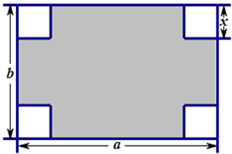 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.科目:czsx 来源: 题型:阅读理解
 (1)如图所示,在△ABC中,AD是BC边上的中线,且AD=
(1)如图所示,在△ABC中,AD是BC边上的中线,且AD=| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
科目:czsx 来源: 题型:
 如图所示,在长和宽分别是a,b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a,b的矩形纸片的四个角都剪去一个边长为x的正方形.科目:czsx 来源: 题型:
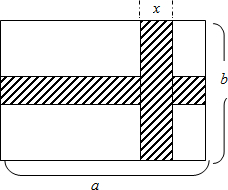 如图所示,在长为a cm,宽为b cm的长方形地面上修两条同样宽的道路,余下部分作为绿化地,若设路宽为x cm.
如图所示,在长为a cm,宽为b cm的长方形地面上修两条同样宽的道路,余下部分作为绿化地,若设路宽为x cm.科目:czsx 来源: 题型:
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.科目:czsx 来源:2013年初中毕业升学考试(浙江衢州卷)数学(带解析) 题型:解答题
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
(1)用a,b,x表示纸片剩余部分的面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
科目:czsx 来源: 题型:
(本小题满分12分)如图所示,在梯形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() 与
与![]() 相切于
相切于![]() .已知
.已知![]() ,边
,边![]() 比
比![]() 大6.
大6.
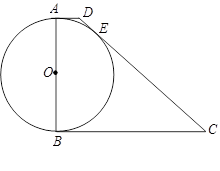
(1)求边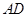 、
、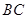 的长.
的长.
(2)在直径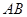 上是否存在一动点
上是否存在一动点 ,使以
,使以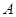 、
、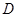 、
、 为顶点的三角形与
为顶点的三角形与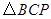 相似?若存在,求出
相似?若存在,求出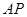 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.