练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知αβγ

    已知αβγ答案解析

    科目：gzsx 来源： 题型：

    如图，某地为了开发旅游资源，欲修建一条连接风景点P和居民区O的公路，点P所在的山坡面与山脚所在水平面α所成的二面角为θ（0°＜θ＜90°），且sinθ=
    2
    5
    ，点P到平面α的距离PH=0.4（km）．沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km，原有公路改建费用为
    a
    2
    万元/km、当山坡上公路长度为lkm（1≤l≤2）时，其造价为（l2+1）a万元、已知OA⊥AB，PB⊥AB，AB=1.5（km），OA=
    		3
    (km)    ．
    （Ⅰ）在AB上求一点D，使沿折线PDAO修建公路的总造价最小；
    （Ⅱ）对于（I）中得到的点D，在DA上求一点E，使沿折线PDEO修建公路的总造价最小．
    （Ⅲ）在AB上是否存在两个不同的点D′，E′，使沿折线PD′E′O修建公路的总造价小于（Ⅱ）中得到的最小总造价，证明你的结论、
    精英家教网

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=
    x2+4xx≥0
    4x-x2x＜0.
    若f（2-a2）＞f（a），则实数a的取值范围是（　　）
    A、（-∞，-1）∪（2，+∞）
    B、（-1，2）
    C、（-2，1）
    D、（-∞，-2）∪（1，+∞）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知正方形ABCD的边长为2，点P为对角线AC上一点，则（
    .
    AP
    +
    .
    BD
    ）•（
    .
    PB
    +
    .
    PD
    ）的最大值为
     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力．每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有60%，参加过计算机培训的有75%．假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响．
    （Ⅰ）任选1名下岗人员，求该人参加过培训的概率；
    （Ⅱ）任选3名下岗人员，记ξ为3人中参加过培训的人数，求ξ的分布列和期望．
     ξ  0  1  2  3
     P  0.021  0.027  0.243  0.729

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=-x3+ax2-x-1在（-∞，+∞）上是单调函数，则实数a的取值范围是（　　）
    A、(-∞，-
    		3
    ]∪[
    		3
    ，+∞)
    B、[-
    		3
    ，
    		3
    ]
    C、(-∞，-
    		3
    )∪(
    		3
    ，+∞)
    D、(-
    		3
    ，
    		3
    )

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=sin(ωx+
    π
    4
    )(x∈R，ω＞0)    的最小正周期为π，为了得到函数g（x）=cosωx的图象，只要将y=f（x）的图象（　　）
    A、向左平移
    π
    8
    个单位长度
    B、向右平移
    π
    8
    个单位长度
    C、向左平移
    π
    4
    个单位长度
    D、向右平移
    π
    4
    个单位长度

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知t=0时刻一质点在数轴的原点，该质点每经过1秒就要向左或向右跳动一个单位长度，已知每次跳动，该质点向左的概率为
    1
    3
    ，向右的概率为
    2
    3
    ．
    （1）求t=3秒时刻，该质点在数轴上x=1处的概率．
    （2）设t=3秒时刻，该质点在数轴上x=ξ处，求Eξ、Dξ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知向量
    a
    与
    b
    的夹角为120°，且|
    a
    |=|
    b
    |=4    ，那么
    b
    •(2
    a
    +
    b
    )    的值为
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知边长为a的菱形ABCD，∠A=
    π
    3
    ，将菱形ABCD沿对角线折成二面角θ，已知θ∈[
    π
    3
    ，
    2π
    3
    ]，则两对角线距离的最大值是（　　）
    A、
    3
    2
    a
    B、
    		3
    4
    a
    C、
    		3
    2
    a
    D、
    3
    4
    a

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=cos2(x+
    π
    12
    )    ，g(x)=1+
    1
    2
    sin2x    ．
    （Ⅰ）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值；
    （Ⅱ）求函数h（x）=f（x）+g（x）的单调递增区间．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=x2+ax-lnx，a∈R．
    （1）若函数f（x）在[1，2]上是减函数，求实数a的取值范围；
    （2）令g（x）=f（x）-x2，是否存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，若存在，求出a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知f（x）是二次函数，不等式f（x）＜0的解集是（0，5），且f（x）在区间[-1，4]上的最大值是12．
    （1）求f（x）的解析式；
    （2）是否存在实数m，使得方程f(x)+
    37x
    =0    在区间（m，m+1）内有且只有两个不等的实数根？若存在，求出m的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设{an}是等差数列，bn=（
    1
    2
    ）an．已知b1+b2+b3=
    21
    8
    ，b1b2b3=
    1
    8
    ．求等差数列的通项an．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知直线l经过点P（1，1），倾斜角α=
    π6
    ，
    （1）写出直线l的参数方程；
    （2）设l与圆x2+y2=4相交于两点A，B，求点P到A，B两点的距离之积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点F1、F2分别是双曲线
    x2
    a2
    -
    y2
    b2
    =1    的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，若△ABF2为锐角三角形，则该双曲线的离心率e的取值范围是（　　）
    A、（1，+∞）
    B、(1，
    		3
    )
    C、（1，2）
    D、(1，1+
    		2
    )

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知随机变量ξ～N(2，  
    1
    2
    )    ，且η=
    ξ-3.5
    		2
    ，则η的方差为
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

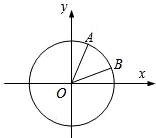    精英家教网如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别交单位圆于A，B两点．已知A，B两点的横坐标分别是
    		2
    10
    ，
    2
    		5
    5
    ．
    （1）求tan（α+β）的值；
    （2）求α+2β的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=
    tanx(x≥0)
    lg(-x)(x＜0)
    ，则f（
    π
    4
    ）•f（-100）=
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知A（-2，0），B（2，0），动点P满足∠APB=θ，且|PA|•|PB|cos2
    θ2
    =4    ．
    （1）求动点P的轨迹C；
    （2）设过M（0，1）的直线l（斜率存在）交P点轨迹C于P、Q两点，B1、B2是轨迹C与y轴的两个交点，直线B1P与B2Q交于点S，试问：当l转动时，点S是否在一条定直线上？若是，请写出这直线的方程，并证明你的结论；若不是，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知ab≠0，点M（a，b）是圆x2+y2=r2内一点，直线m是以点M为中点的弦所在的直线，直线l的方程是ax+by=r2，则下列结论正确的是（　　）
    A、m∥l，且l与圆相交B、l⊥m，且l与圆相切C、m∥l，且l与圆相离D、l⊥m，且l与圆相离

    查看答案和解析>>