
题目列表(包括答案和解析)
| ||
| 7 |
| ||
| 7 |
| MA |
| MB |
| MC |
| 0 |
| NC |
| 7 |
| NA |
| 7 |
| NB |
| MN |
| AB |
| PE |
| PF |
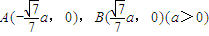 ,两动点M、N满足
,两动点M、N满足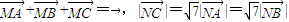 ,向量
,向量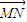 与
与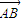 共线.
共线.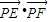 的取值范围.
的取值范围.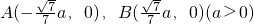 ,两动点M、N满足
,两动点M、N满足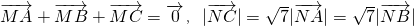 ,向量
,向量 与
与 共线.
共线. 的取值范围.
的取值范围.(1)求△ABC的顶点C的轨迹;
(2)若过点P(0,a)的直线与点C的轨迹相交于E、F两点,求![]() ·
·![]() 的取值范围;
的取值范围;
(3)若G(-a,0),H(2a,0),Q点为C点轨迹在第一象限内的任意一点,则是否存在常数λ(λ>0),使得∠QHG=λ∠QGH恒成立?若存在,求出λ的值;若不存在,请说明理由.
 |=2且EF⊥l于G,点Q是直线l上一动点,点M满足
|=2且EF⊥l于G,点Q是直线l上一动点,点M满足 =0.
=0. π≤θ<π时,求直线l1的斜率k的取值范围.
π≤θ<π时,求直线l1的斜率k的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com