
题目列表(包括答案和解析)
(12分)如图,在正四棱柱ABCD―A1B1C1D1中,AA1=![]() AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B―A1N―B1的正切值.

(12分)如图,已知圆C:![]() ,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足![]() =
=![]() ,
,![]() ?
?![]() =0,点N的轨迹为曲线E.
=0,点N的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若过定点A(1,0)的直线![]() 交曲线E于不同的两点G、H,
交曲线E于不同的两点G、H,
且满足∠GOH为锐角,求直线![]() 的斜率k的取值范围.
的斜率k的取值范围.

(12分)直角梯形ABCD中, ∠DAB=90°,AD//BC,
AB=2, AD=![]() , BC=
, BC=![]() ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:![]() ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线![]() 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线![]() 的斜率
的斜率![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(12分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;(6分)
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X). (6分)
(12分)如图,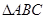 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E
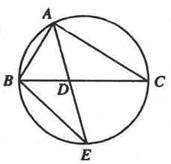
(I)证明: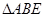
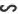
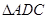
(II)若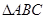 的面积
的面积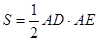 ,求
,求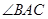 的大小。
的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com