
题目列表(包括答案和解析)
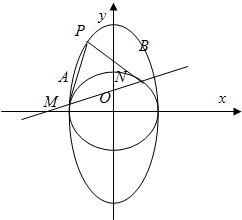 附加题:如图,过椭圆C:
附加题:如图,过椭圆C:| y2 |
| a2 |
| x2 |
| b2 |
| a2 |
| |OM|2 |
| b2 |
| |ON|2 |
| 25 |
| 16 |
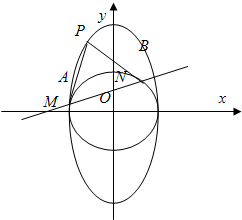 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: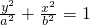 (a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.
(a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.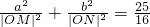 ,求椭圆C的方程;
,求椭圆C的方程;(本题16分,其中第(1)小题8分,第(2)小题8分)
已知椭圆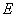 的方程为
的方程为 ,长轴是短轴的2倍,且椭圆
,长轴是短轴的2倍,且椭圆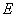 过点
过点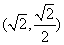 ;斜率为
;斜率为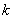 的直线
的直线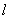 过点
过点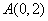 ,
,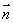 为直线
为直线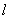 的一个法向量,坐标平面上的点
的一个法向量,坐标平面上的点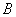 满足条件
满足条件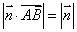 .
.
(1)写出椭圆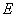 方程,并求点
方程,并求点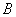 到直线
到直线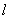 的距离;
的距离;
(2)若椭圆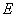 上恰好存在3个这样的点
上恰好存在3个这样的点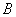 ,求
,求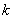 的值.
的值.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式![]() :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点![]() 变换到这一平面上的一点
变换到这一平面上的一点![]() .
.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2) 若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换![]() 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2) 若曲线 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线 在变换
在变换 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
一、选择题
1、C 2、C 3、D 4、B 5、D 6、A
7、D 8、B 9、C 10、A 11、B 12、B
二、填空题
13、±4 14、0.18 15、251,4 16、①②
三、解答题
17、解:(Ⅰ)由 ,得
,得
即 
也即

∴
∴ ∴
∴
(Ⅱ)∵


∴ 的最大值为
的最大值为
18、解:(Ⅰ)∵击中目标 次的概率为
次的概率为
∴他至少击中两次的概率
(Ⅱ)设转移前射击次数为 ,
, 的可能取值为1,2,3,4,5
的可能取值为1,2,3,4,5
则 ,
, 1,2,3,4
1,2,3,4 
∴ 的分布列为
的分布列为

1
2
3
4
5






∴
19、解:(Ⅰ)∵ 面
面 ,∴
,∴ 面
面
|