设函数f（x）=lnx，g（x）=ax+，函数f（x）的图像与x轴的交点也在函数g（x）的图像上，且在此点处f（x）与g（x）有公切线.[来源:学。科。网]

（Ⅰ）求a、b的值； 

（Ⅱ）设x>0，试比较f（x）与g（x）的大小.[来源:学,科,网Z,X,X,K]

【解析】第一问解：因为f（x）=lnx，g（x）=ax+

则其导数为

由题意得，

第二问，由（I）可知，令。

∵，  …………8分

∴是（0，+∞）上的减函数，而F（1）=0，            …………9分

∴当时，，有；当时，，有；当x=1时，，有

解：因为f（x）=lnx，g（x）=ax+

则其导数为

由题意得，

（11）由（I）可知，令。

∵，  …………8分

∴是（0，+∞）上的减函数，而F（1）=0，            …………9分

∴当时，，有；当时，，有；当x=1时，，有

设函数

（1）当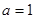时，求曲线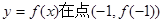处的切线方程；

（2）当时，求的极大值和极小值；

（3）若函数在区间上是增函数，求实数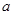的取值范围.

【解析】（1）中，先利用，表示出点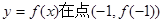的斜率值这样可以得到切线方程。（2）中，当，再令，利用导数的正负确定单调性，进而得到极值。（3）中，利用函数在给定区间递增，说明了在区间导数恒大于等于零，分离参数求解范围的思想。

解：（1）当……2分

    ∴

即为所求切线方程。………………4分

（2）当

令………………6分

∴递减，在（3，+）递增

∴的极大值为…………8分

（3）

①若上单调递增。∴满足要求。…10分

②若

∵恒成立，

恒成立，即a>0……………11分

时，不合题意。综上所述，实数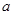的取值范围是

已知函数

（1）若函数的图象经过P（3，4）点，求a的值；

（2）比较大小，并写出比较过程；

（3）若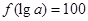，求a的值.

【解析】本试题主要考查了指数函数的性质的运用。第一问中，因为函数的图象经过P（3，4）点，所以，解得，因为，所以.

（2）问中，对底数a进行分类讨论，利用单调性求解得到。

（3）中，由知，.，指对数互化得到，，所以，解得所以， 或 .

解：⑴∵函数的图象经过∴，即.        … 2分

又，所以.             ………… 4分

⑵当时，;

当时，. ……………… 6分

因为，，

当时，在上为增函数，∵，∴.

即.当时，在上为减函数，

∵，∴.即.      …………………… 8分

⑶由知，.所以，（或）.

∴.∴，       … 10分

∴ 或 ，所以， 或 .

已知，函数

（1）当时，求函数在点(1，)的切线方程；

(2)求函数在[－1，1]的极值；

(3)若在上至少存在一个实数x₀，使>g(x_o)成立，求正实数的取值范围。

【解析】本试题中导数在研究函数中的运用。（1）中，那么当时，  又    所以函数在点(1，)的切线方程为；（2）中令   有 

对a分类讨论，和得到极值。（3）中，设，，依题意，只需那么可以解得。

解：（Ⅰ）∵  ∴

∴  当时，  又    

∴  函数在点(1，)的切线方程为 --------4分

（Ⅱ）令   有 

①         当即时

故的极大值是，极小值是

②         当即时，在（－1,0）上递增，在（0,1）上递减，则的极大值为，无极小值。 

综上所述   时，极大值为，无极小值

时  极大值是，极小值是        ----------8分

（Ⅲ）设，

对求导，得

∵，    

∴ 在区间上为增函数，则

依题意，只需，即 

解得  或（舍去）

则正实数的取值范围是（，）

（本题满分8分）探究函数的最小值，并确定相应的x的值，列表如下：

请观察表中y值随x值变化的特点，完成下列问题：

(Ⅰ)若，则    （请填写“>, =, <”号）；若函数,(x>0)在区间(0,2)上递减，则在         上递增；

(Ⅱ)当x=       时，,(x>0)的最小值为         ；

(Ⅲ)试用定义证明,(x>0)在区间(0,2)上递减．