一家保险公司调查其总公司营业部的加班程度,收集了10周中每周加班工作时间y(小时)与签发新保单数目x的数据如下表,则用最小二乘估计求出的回归直线方程是___________.

x	825	215	1 070	550	480	920	1 350	325	670	1 215
y	3.5	1.0	4.0	2.0	1.0	3.0	4.5	1.5	3.0	5.0

（1）一家保险公司调查其总公司营业部的加班程度，收集了10周中每周加班工作时间y（小时）与签发新保单数目x的数据如下表，则用最小二乘估计求出的回归直线方程是 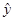   =0.1181+0.003585x            .

x	825	215	1070	550	480	920	1350	325	670	1215
y	3.5	1.0	4.0	2.0	1.0	3.0	4.5	1.5	3.0	5.0

（2）上题中，每周加班时间y与签发新保单数目x之间的相关系数    ，查表得到的相关系数临界值r_0.05=          ，这说明题中求得的两变量之间的回归直线方程是          （有／无）意义的．

（3）上面题中，若该公司预计下周签发新保单1000张，需要的加班时间的估计是           .

 

以下是收集到的新房屋的销售价格y和房屋的大小x的数据:

房屋大小(m2)	115	110	80	135	105
销售价格(万元)	24.8	21.6	18.4	29.2	22

(1)画出数据的散点图;

(2)用最小二乘估计求线性回归方程,并在散点图中加上回归直线;

(3)计算残差平方和、总偏差平方和及相关指数R²,并指出预报变量的变化在多大程度上与解释变量有关?在多大程度上与残差变量有关?

以下是收集到的新房屋的销售价格y和房屋的大小x的数据.

房屋大小/m2	115	110	80	135	105
销售价格/万元	24.8	21.6	18.4	29.2	22

(1)画出数据的散点图;

(2)用最小二乘估计求线性回归方程；

(3)求相关系数r,并作出评价.

下面是上海市统计局提供的主要年份的研究生人数情况．

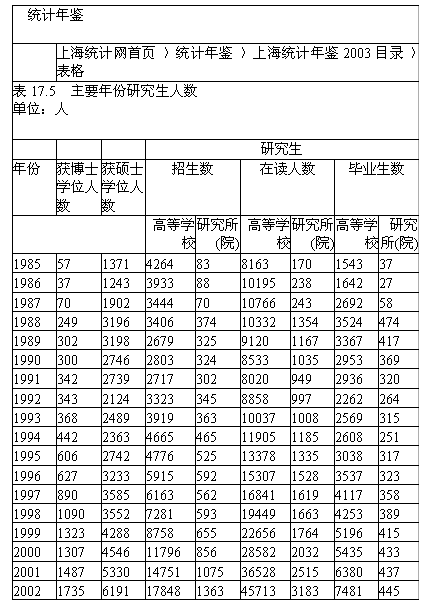
(1)画出获硕士学位人数和获博士学位人数之间的散点图．

(2)上面的二者之间是否是线性相关的？如果是，请用最小二乘估计求出博士学位人数关于硕士学位人数的线性回归方程．

(3)如果2005年获硕士学位人数为10000人，请估计获博士学位的人数．

(4)如果硕士研究生的在读时间为3年，当年获硕士学位的人数与第三年后获博士学位的人数之间应当有一个什么关系？请画出散点图，如果成线性关系，用最小二乘法给出线性回归方程．

(5)比较(4)中的回归方程与(2)中的回归方程之间的差异，你认为哪个方程更具有代表性？

(6)请试着分析其他数据之间的关系．