
题目列表(包括答案和解析)
给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;③  的递增区间为
的递增区间为 ;④定义在R上的函数
;④定义在R上的函数 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有 成立,则
成立,则 在R上是增函数;⑤
在R上是增函数;⑤ 的单调减区间是
的单调减区间是 ;正确的有____________
;正确的有____________
给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;③  的递增区间为
的递增区间为 ;④定义在R上的函数
;④定义在R上的函数 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有 成立,则
成立,则 在R上是增函数;⑤
在R上是增函数;⑤ 的单调减区间是
的单调减区间是 ;正确的有____________
;正确的有____________
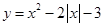 的递增区间为
的递增区间为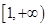 ;④定义在R上的函数
;④定义在R上的函数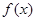 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有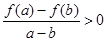 成立,则
成立,则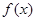 在R上是增函数;⑤
在R上是增函数;⑤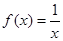 的单调减区间是
的单调减区间是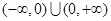 ;正确的有____________
;正确的有____________给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;③y=x2-2|x-3|的递增区间为[1,+∞);④定义在R上的函数f(x)对任意两个不等实数a、b,总有![]() >0成立,则f(x)在R上是增函数;⑤f(x)=
>0成立,则f(x)在R上是增函数;⑤f(x)=![]() 的单调减区间是(-∞,0)∪(0,+∞);正确的有________.
的单调减区间是(-∞,0)∪(0,+∞);正确的有________.
| f(a)-f(b) |
| a-b |
| 1 |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com