
题目列表(包括答案和解析)
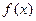
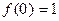
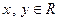
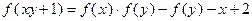 .
.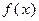 的解析式;
的解析式;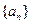 满足:
满足: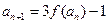 (
(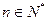 ),且
),且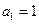 , 求数列
, 求数列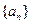 的通项;
的通项;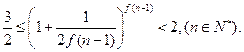
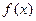
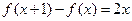
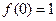
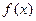 的解析式;
的解析式;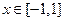 时,不等式:
时,不等式: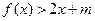 恒成立,求实数
恒成立,求实数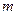 的范围.
的范围.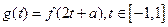
 ,求
,求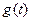 的最大值;
的最大值;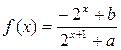
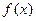 的解析式;
的解析式;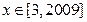 ,不等式
,不等式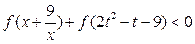 恒成立,求t
恒成立,求t| 1 |
| x |
| x |
| 1-x2 |
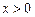 时,
时,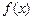 的解析式;
的解析式;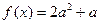 有三个不同的解,求a的取值范围。
有三个不同的解,求a的取值范围。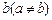 ,当
,当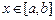 时,
时,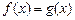 ,且
,且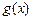 的值域为
的值域为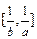 .若存在,求出a、b 的值;若不存在,说明理由
.若存在,求出a、b 的值;若不存在,说明理由卷Ⅰ(必修1部分,满分100分)
一、填空题(每小题5分,共45分)
1..files/image153.gif) 2.
2..files/image155.gif) 3.
3. .files/image157.gif) 4.
4. .files/image159.gif) 5.
5..files/image161.gif)
6..files/image163.gif) 7.
7. .files/image165.gif) 8.
8..files/image167.gif) 9.
9..files/image169.gif)
二、解答题(共55分)
10..files/image171.gif) ,
,.files/image173.gif)
11.解:⑴设.files/image175.gif) ,由
,由.files/image067.gif) ,得
,得.files/image178.gif) ,故
,故.files/image180.gif) .
.
因为.files/image065.gif) ,所以
,所以.files/image182.gif) .
.
即.files/image184.gif) ,所以
,所以.files/image186.gif) ,即
,即.files/image188.gif) ,所以
,所以.files/image190.gif) .
.
⑵由题意得.files/image192.gif) 在
在.files/image194.gif) 上恒成立,即
上恒成立,即.files/image196.gif) 在
在.files/image194.gif) 上恒成立.
上恒成立.
设.files/image198.gif) ,其图象的对称轴为直线
,其图象的对称轴为直线.files/image200.gif) ,
,
所以.files/image202.gif) 在
在.files/image194.gif) 上递减,所以当
上递减,所以当.files/image204.gif) 时,
时,.files/image202.gif) 有最小值
有最小值.files/image207.gif) .故
.故.files/image209.gif) .
.
12.解:⑴设一次订购量为.files/image030.gif) 个时,零件的实际出厂价恰好为
个时,零件的实际出厂价恰好为.files/image212.gif) 元,则
元,则.files/image214.gif) (个)
(个)
⑵.files/image216.gif)
⑶当销售一次订购量为.files/image076.gif) 个时,该工厂的利润为
个时,该工厂的利润为.files/image219.gif) ,则
,则
.files/image221.gif)
故当.files/image223.gif) 时,
时,.files/image225.gif) 元;
元;.files/image227.gif) 元.
元.
13.解:⑴由已知条件得.files/image229.gif) 对定义域中的
对定义域中的.files/image076.gif) 均成立.
均成立.
.files/image232.gif)
.files/image234.gif) ,即
,即.files/image236.gif) .
.
.files/image232.gif)
.files/image238.gif) 对定义域中的
对定义域中的.files/image076.gif) 均成立.
均成立. .files/image232.gif)
.files/image240.gif) ,即
,即.files/image242.gif) (舍正),所以
(舍正),所以.files/image244.gif) .
.
⑵由⑴得.files/image246.gif) .设
.设.files/image248.gif) ,
,
.files/image232.gif) 当
当.files/image250.gif) 时,
时,.files/image252.gif) ,
,.files/image232.gif)
.files/image254.gif) .
.
当.files/image256.gif) 时,
时,.files/image258.gif) ,即
,即.files/image260.gif) .
..files/image232.gif) 当
当.files/image256.gif) 时,
时,.files/image063.gif) 在
在.files/image088.gif) 上是减函数.
上是减函数.
同理当.files/image264.gif) 时,
时,.files/image063.gif) 在
在.files/image088.gif) 上是增函数.
上是增函数.
⑶.files/image266.gif) 函数
函数.files/image063.gif) 的定义域为
的定义域为.files/image268.gif) ,
,
.files/image232.gif) ①
①.files/image270.gif) ,
,.files/image232.gif)
.files/image264.gif) .
..files/image232.gif)
.files/image063.gif) 在
在.files/image272.gif) 为增函数,要使值域为
为增函数,要使值域为.files/image088.gif) ,
,
则.files/image275.gif) (无解)
(无解)
②.files/image277.gif) ,
, .files/image232.gif)
.files/image279.gif)
.files/image232.gif)
.files/image063.gif) 在
在.files/image272.gif) 为减函数,
为减函数,
要使.files/image063.gif) 的值域为
的值域为.files/image088.gif) , 则
, 则.files/image285.gif) .
..files/image232.gif)
.files/image287.gif) ,
,.files/image289.gif) .
.
卷Ⅱ(必修4部分,满分60分)
一、填空题(每小题6分,共30分)
1..files/image291.gif) 2.
2. .files/image291.gif) 3.
3.
.files/image293.gif) 4.
4.
.files/image295.gif) 5.
②③
5.
②③
二、解答题(共30分)
6. ⑴.files/image297.gif) ;
;
⑵对称中心:.files/image299.gif) ,增区间:
,增区间:.files/image301.gif) ,
,
⑶.files/image303.gif) .
.
7.解:⑴.files/image305.gif) ,
,
当.files/image256.gif) 时,则
时,则.files/image308.gif) 时,
时,.files/image310.gif) ;
;
当.files/image312.gif) 时,则
时,则.files/image314.gif) 时,
时,.files/image316.gif) ;
;
当.files/image318.gif) 时,则
时,则.files/image320.gif) 时,
时,.files/image322.gif) ;
;
记.files/image324.gif) ,则
,则.files/image326.gif) .
.
⑵若.files/image149.gif) ,则
,则.files/image329.gif) ;若
;若.files/image331.gif) 解之,得
解之,得.files/image333.gif) (舍),
(舍),.files/image335.gif) ;若
;若.files/image337.gif) ,则
,则.files/image335.gif) (舍).
(舍).
综上所述,.files/image335.gif) 或
或.files/image329.gif)
⑶当.files/image335.gif) 时,
时,.files/image339.gif) ,即当
,即当.files/image341.gif) 时,
时,.files/image343.gif) ;
;
当.files/image329.gif) 时,
时,.files/image345.gif) ,即当
,即当.files/image347.gif) 时,
时,.files/image349.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com