
题目列表(包括答案和解析)
1.探究新知
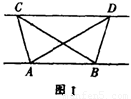
如图1,已知ΔABC与ΔABD的面积相等,试判断AB与CD的位置关系,并说明理由;[来源:

2.结论应用:
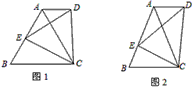
如图2,过点M,N在反比例函数![]() 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明MN//EF。
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明MN//EF。

1.探究新知
如图1,已知ΔABC与ΔABD的面积相等,试判断AB与CD的位置关系,并说明理由;[来源:
2.结论应用:
如图2,过点M,N在反比例函数 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明MN//EF。
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明MN//EF。

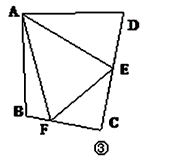
 ∠DAB,试猜想DE,BF,EF之间有何数量关系,并证明你的猜想;
∠DAB,试猜想DE,BF,EF之间有何数量关系,并证明你的猜想; ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF,请直接写出你的猜想(不必说明理由)。
∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF,请直接写出你的猜想(不必说明理由)。 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com