
2.在等比数列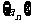 ,已知
,已知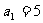 ,
,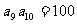 ,求
,求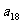 .
.
1.求下列各等比数列的通项公式:
1) a1=-2, a3=-8
2) a1=5, 且2an+1=-3an
3)
a1=5, 且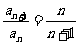
[例1] 已知数列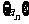 的前n项之和Sn=aqn(
的前n项之和Sn=aqn(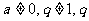 为非零常数),则
为非零常数),则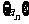 为( )。
为( )。
A.等差数列 
B.等比数列 
C.既不是等差数列,也不是等比数列
D.既是等差数列,又是等比数列
错解: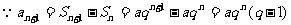

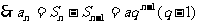
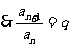 (常数)
(常数)
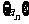 为等比数列,即B。
为等比数列,即B。
错因:忽略了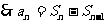 中隐含条件n>1.
中隐含条件n>1.
正解:当n=1时,a1=S1=aq;
当n>1时,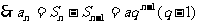
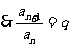 (常数)
(常数)
但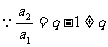
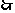
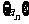 既不是等差数列,也不是等比数列,选C。
既不是等差数列,也不是等比数列,选C。
[例2] 已知等比数列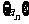 的前n项和记为Sn,S10=10 ,S30=70,则S40等于.
的前n项和记为Sn,S10=10 ,S30=70,则S40等于.
错解:S30= S10·q 2. 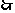 q 2=7,q=
q 2=7,q=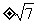 ,
,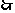 S40=
S30·q =
S40=
S30·q =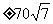 .
.
错因:是将等比数列中Sm, S2m -Sm, S3m -S2m成等比数列误解为Sm, S2m, S3m成等比数列.
正解:由题意: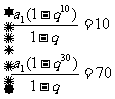 得
得 ,
,
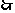 S40=
S40=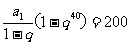 .
.
[例3] 求和:a+a2+a3+…+an.
错解: a+a2+a3+…+an=
a+a2+a3+…+an=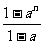 .
.
错因:是(1)数列{an}不一定是等比数列,不能直接套用等比数列前n项和公式(2)用等比数列前n项和公式应讨论q是否等于1.
正解:当a=0时,a+a2+a3+…+an=0;
当a=1时,a+a2+a3+…+an=n;
当a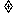 1时,
1时, a+a2+a3+…+an=
a+a2+a3+…+an=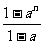 .
.
[例4]设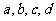 均为非零实数,
均为非零实数,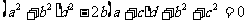 ,
,
求证: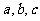 成等比数列且公比为
成等比数列且公比为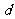 。
。
证明:
证法一:关于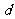 的二次方程
的二次方程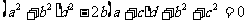 有实根,
有实根,
∴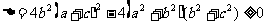 ,∴
,∴
则必有: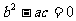 ,即
,即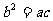 ,∴非零实数
,∴非零实数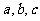 成等比数列
成等比数列
设公比为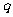 ,则
,则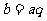 ,
,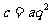 代入
代入
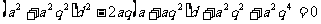
∵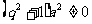 ,即
,即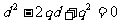 ,即
,即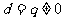 。
。
证法二:∵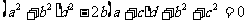
∴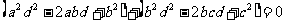
∴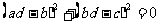 ,∴
,∴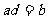 ,且
,且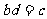
∵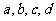 非零,∴
非零,∴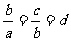 。
。
[例5]在等比数列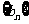 中,
中,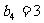 ,求该数列前7项之积。
,求该数列前7项之积。
解: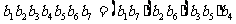
∵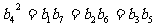 ,∴前七项之积
,∴前七项之积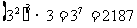
[例6]求数列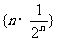 前n项和
前n项和
解: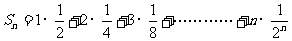 ①
①
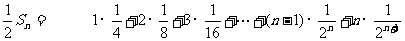 ②
②
两式相减: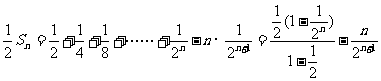
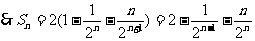
[例7]从盛有质量分数为20%的盐水2kg的容器中倒出1kg盐水,然后加入1kg水,以后每次都倒出1kg盐水,然后再加入1kg水,
问:(1)第5次倒出的的1kg盐水中含盐多kg?
(2)经6次倒出后,一共倒出多少kg盐?此时加1kg水后容器内盐水的盐的质量分数为多少?
解:(1)每次倒出的盐的质量所成的数列为{an},则:
a1=
0.2 (kg), a2=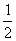 ×0.2(kg), a3= (
×0.2(kg), a3= (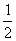 )2×0.2(kg)
)2×0.2(kg)
由此可见:an= (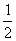 )n-1×0.2(kg), a5= (
)n-1×0.2(kg), a5= (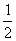 )5-1×0.2=
(
)5-1×0.2=
(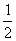 )4×0.2=0.0125(kg)。
)4×0.2=0.0125(kg)。
(2)由(1)得{an}是等比数列 a1=0.2 , q=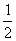
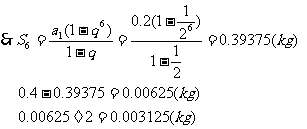
答:第5次倒出的的1kg盐水中含盐0.0125kg;6次倒出后,一共倒出0.39375kg盐,此时加1kg水后容器内盐水的盐的质量分数为0.003125。
7.在解决等比数列问题时,如已知,a1,an,d,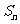 ,n中任意三个,可求其余两个。
,n中任意三个,可求其余两个。
6.等比数列{an}的通项公式an=a1qn-1可改写为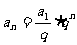 .当q>0,且q
.当q>0,且q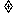 1时,y=qx是一个指数函数,而
1时,y=qx是一个指数函数,而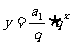 是一个不为0 的常数与指数函数的积,因此等比数列{an}的图象是函数
是一个不为0 的常数与指数函数的积,因此等比数列{an}的图象是函数 的图象上的一群孤立的点.
的图象上的一群孤立的点.
5.在已知等比数列中任意两项的前提下,使用an=amqn-m可求等比数列中任意一项.
4.在已知等比数列的a1和q的前提下,利用通项公式an=a1qn-1,可求出等比数列中的任一项.
3.“从第2项起”是因为首项没有“前一项”,同时应注意如果一个数列不是从第2项起,而是从第3项或第4项起每一项与它前一项的比都是同一个常数,此数列不是等比数列,这时可以说此数列从. 第2项或第3项起是一个等比数列.
2.对于公比q,要注意它是每一项与它前一项的比,防止把相邻两项的比的次序颠倒.
1.由于等比数列的每一项都可能作分母,故每一项均不为0,因此q也不为0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com