
1. 回旋加速器解读
例1. (2005天津高考)正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段。
(1)PET在心脏疾病诊疗中,需要使用放射正电子的同位素氮13示踪剂,氮13是由小型回旋加速器输出的高速质子轰击氧16获得的,反应中同时还产生另一个粒子,试写出该核反应方程。
(2)PET所用回旋加速器示意如图1,其中置于高真空中的金属D形盒的半径为R,两盒间距为d,在左侧D形盒圆心处放有粒子源S,匀强磁场的磁感应强度为B,方向如图所示。质子质量为m,电荷量为q。设质子从粒子源S进入加速电场时的初速度不计,质子在加速器中运动的总时间为t(其中已略去了质子在加速电场中的运动时间),质子在电场中的加速次数于回旋半周的次数相同,加速质子时的电压大小可视为不变。求此加速器所需的高频电源频率f和加速电压U。

图1
(3)试推证当 时,质子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计(质子在电场中运动时,不考虑磁场的影响)。
时,质子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计(质子在电场中运动时,不考虑磁场的影响)。
解析:
(1)核反应方程为: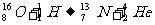 ①
①
(2)设质子加速后最大速度为v,由牛顿第二定律得:
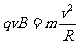 ②
②
质子的回旋周期为: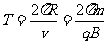 ③
③
高频电源的频率为: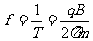 ④
④
质子加速后的最大动能为: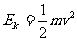 ⑤
⑤
设质子在电场中加速的次数为n,则:
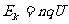 ⑥
⑥
又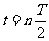 ⑦
⑦
可解得: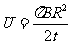 ⑧
⑧
(3)在电场中加速的总时间为:
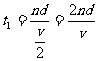 ⑨
⑨
在D形盒中回旋的总时间为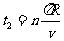 ⑩
⑩
故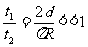 ,即当
,即当 时,
时,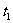 可以忽略不计。
可以忽略不计。
评点:交变电场的周期等于带电粒子在磁场中做匀速圆周运动的周期,经交变电场每半周粒子被加速一次。
避免分类讨论的解题策略:分类讨论的思想是一种重要的解题策略,对于培养学生思维的严密性,严谨性和灵活性以及提高学生分析问题和解决问题的能力无疑具有较大的帮助。然而并不是问题中一出现含参数问题就一定得分类讨论,如果能结合利用数形结合的思想,函数的思想等解题思想方法可避免或简化分类讨论,从而达到迅速、准确的解题效果。
练习1、若函数f(x)=a+bcosx+csinx的图象经过点(0,1)和(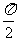 ,1)两点,且x∈[0,
,1)两点,且x∈[0,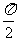 ]时,|f(x)|≤2恒成立,试求a的取值范围。
]时,|f(x)|≤2恒成立,试求a的取值范围。
练习2、已知函数f(x)=sim2x-asim2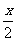
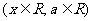
试求以a表示f(x)的最大值b。
练习3、 若不等式 Cos2x-mCosx+2m-2>0的解集为(0,Л/2),求实数m的取值范围.
4、 “正难则反,补集思想应用”可简化或避免分类.
例4、 若二次函数f(x)=mx2+(m-3)x+1的图象与x轴的交点中至少有一个在x的正半轴上,求m的取值范围.
当堂检测:关于实数x的不等式 与
与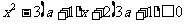 的解集依次记为
的解集依次记为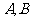 ,求使
,求使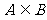 的a的取值范围.
的a的取值范围.
课堂小结
[分类讨论的经典问题回放]
1某些概念和函数的性质常常导致分类
例1设为实数,函数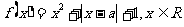 ⑴ 讨论
⑴ 讨论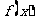 奇偶性;⑵ 求函数
奇偶性;⑵ 求函数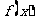 的最小值.
的最小值.
2 “二次问题”常常借助两根的大小或判别式分类
例2.设不等式x2-2ax+a+2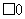 的解集为M,且M
的解集为M,且M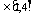 ,求实数a的范围.
,求实数a的范围.
3、由图形位置的不确定而导致分类.
例3、四面体的四个顶点到平面M的距离之比为1:1:1:3,求满足条件的平面M的个数.
[思想方法精析]
分类讨论思想是一种“化繁为简、化整为零,分别对待,各个击破,再积零为整”的思维策略.
运用分类讨论思想,应把握分类原则、分类方法和注重分类原因的探讨.
1 引起分类讨论原因的探究.
引起分类讨论的原因大致可归结为:涉及数学概念是分类定义的;运用数学定理、公式、或运算性质、法则是分类给出的;求解的数学问题的结论有多种情况或多种可能性;数学问题中含参数,这些参数不同的取值导致不同的结果;较复杂或非常规的数学问题,需要采用分类讨论的解题策略来解决.
2 分类讨论必须遵循的原则.
施行分类的集合的全集必须是确定的;每一次分类的标准必须是同一的;分类是完备的“彼此的交集为空集,彼此的并集为全集”;若多次分类,必须逐级进行,不能越级.
3 分类讨论的方法.
明确分类的对象,确定对象的全体;确定分类的标准,正确分类;逐类进行讨论,获得阶段性的结果;归纳小结,综合结论.
4 简化或避免分类讨论的策略.
化参数为主元,函数思想应用;正难则反,补集思想的应用;换元法;数形结合法.
22.设数列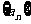 是等比数列,
是等比数列,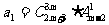 ,公比
,公比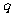 是(
是(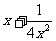 )4的展开式中的第二项(按x的降幂排列)
)4的展开式中的第二项(按x的降幂排列)
(1)
用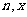 表示通项
表示通项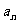 与前n项和
与前n项和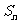 ;
;
(2)
若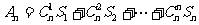 ,用
,用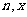 表示
表示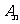 。
。
21.已知: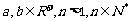 .求证:
.求证: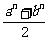 ≥
≥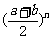
20.已知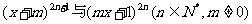 的展开式中含xn项的系数相等,求实数m的取值范围.
的展开式中含xn项的系数相等,求实数m的取值范围.
19.二项式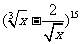 的展开式中:⑴求常数项;⑵有几个有理项;⑶有几个整式项。
的展开式中:⑴求常数项;⑵有几个有理项;⑶有几个整式项。
18.某学习小组有8个同学,从男生中选2人,女生中选1人参加数学、物理、化学三种竞赛,要求每科均有1人参加,共有180种不同的选法,那么该小组中男、女同学各有多少人?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com