
28.在△ABC中,a、b、c分别是∠A、∠B、∠C的对边长,已知a、b、c成等比数列,且a2-c2=ac-bc,求∠A的大小及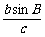 的值.
的值.
解:∵a、b、c成等比数列,∴b2=ac
又a2-c2=ac-bc,∴b2+c2-a2=bc 在△ABC中,由余弦定理得
cosA=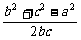 =
=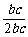 =
=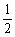 ,∴∠A=60°.
,∴∠A=60°.
在△ABC中,由正弦定理得sinB=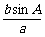 ,
,
∵b2=ac,∠A=60°,∴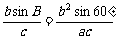 =sin60°=
=sin60°=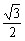 .
.
27.已知函数f(x)=-x3+3x2+9x+a,
(1)求f(x)的单调区间;(2)若f(x)在区间[-2,2]上的最大值为20,求函数f(x)在该区间上的最小值.
解:(1)f′(x)=-3x2+6x+9,令f′(x)<0,解得x<-1或x>3,所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞);
令f′(x)>0,解得-1<x<3,所以函数f(x)的单调递增区间为(-1,3).
(2)因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).因为在区间(-1,3)上,f′(x)>0,所以f(x)在(-1,2)上单调递增.
又由于f(x)在(-2,-1)上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是有22+a=20,解得a=-2,故f(x)=-x3+3x2+9x-2,因此f(-1)=-7,即函数f(x)在区间[-2,2]上的最小值为-7.
26.已知函数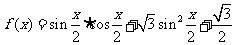 .
.
(Ⅰ)求函数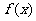 的最小正周期,并写出函数
的最小正周期,并写出函数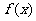 图象的对称轴方程;
图象的对称轴方程;
(Ⅱ)若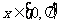 ,求函数
,求函数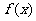 的值域.
的值域.
解:(Ⅰ)因为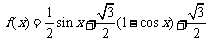
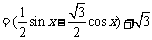
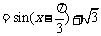 , 所以, 函数
, 所以, 函数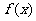 的最小正周期为2
的最小正周期为2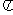 .
.
由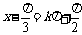 ,得
,得
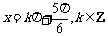 .
.
故函数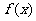 图象的对称轴方程为
图象的对称轴方程为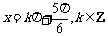 . ………………8分
. ………………8分
(Ⅱ)因为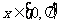 ,所以
,所以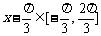 .所以
.所以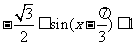 .所以函数
.所以函数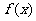 的值域为
的值域为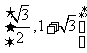 .
………………13分
.
………………13分
25.已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项; (Ⅱ)求数列{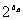 }的前n项和Sn.
}的前n项和Sn.
解 (Ⅰ)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列得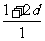 =
=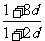 ,
,
解得d=1,d=0(舍去), 故{an}的通项an=1+(n-1)×1=n.
(Ⅱ)由(Ⅰ)知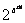 =2n,由等比数列前n项和公式得
=2n,由等比数列前n项和公式得
Sm=2+22+23+…+2n=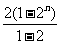 =2n+1-2.
=2n+1-2.
24.若正数x,y满足2x+3y=1,则+的最小值为 .解:5+2
23.计算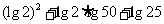 =
=
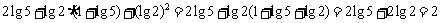
22.数列{an}的前n项和Sn=n 2+2 n-1 则a5+a4=. 解:
21.函数 ,则
,则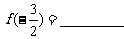 ,若
,若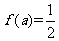 ,则实数
,则实数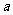 的取值范围是 .
的取值范围是 .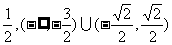
20. 函数
函数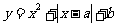 在区间
在区间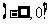 上为减函数,则a的取值范围是
(A)
上为减函数,则a的取值范围是
(A)
(A)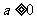 (A)
(A)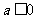 (C)
(C)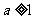 (D)
(D)
19.若变量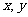 满足约束条件
满足约束条件 则
则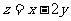 的最大值为( B )
的最大值为( B )
(A)4 (B)3 (C)2 (D)1
 [解析]画出可行域(如右图),
[解析]画出可行域(如右图),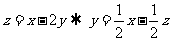 ,由图可知,当直线
,由图可知,当直线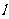 经过点A(1,-1)时,z最大,且最大值为
经过点A(1,-1)时,z最大,且最大值为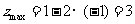 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com