3、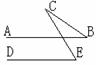选择

(1)　　　 如图，AB∥DE，∠E=65°，则∠B+∠C的度数是(　 )

(A)135°　 (B)115°　 (C)65°　 (D)35°

(2)　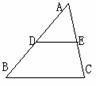　　 如图，D、E分别为△ABC的中点，BC＝8 ∠A=41°，

∠B=48°则下列结论正确的是(　 )

(A)DE=4，∠AED=41°(B)DE=4，∠AED =81°

(C)DE=4，∠AED=48°(D)DE=4，∠ADE=48°

(3)一个角的补角与它的余角的和比这个角的2倍少30°，则这个角等于(　 )

(A)30°　 (B)45°　 (C)60°　 (D)75°

2、判断

(1)若∠A与∠B是同旁内角，则∠A+∠B=180°　　　　　(　)

(2)若∠α与∠β是互为余角，则∠α+∠β=180°　　　　(　)

(3)若∠1=∠2，则∠1与∠2是对顶角　　　　　　　(　)

(4)若两个三角形有两条边及一个角对应相等，则这两个三角形全等　(　)

1、　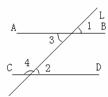 填空：

(1)如图，AB∥CD，∠1＝38°，则∠2＝　　 　　∠3＝　　 　　

∠4＝　　

(2)△ABC中，AB＝3　 BC＝5，则AC的取值范围是　　　

(3)△ABC中，∠A＝30°　 ∠B－∠C＝20°，则∠B＝　　　∠C＝　　

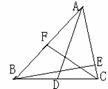(4)添加条件，使线段满足题意：

①、　　　　　　　　 ，AD为△ABC的中线

②、　　　　　　　　 ，BE为△ABC的高

③、　　　　　　　　 ，CF为△ABC的角平分线

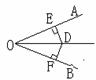(5)已知，OP平分∠AOB，D为OP上一点，DE⊥OA于E，

　 DF⊥OB于F，OD＝5，DE＝3，则DF＝　　　 OF＝　　　

3、　 能综合应用所学知识解决问题.

复习教学过程设计：

2、　 会求一个角的补角、余角，并能利用补角、余角的性质计算或证明；会根据三角形的有关概念计算或证明；会利用平行线的性质计算或证明；会利用全等三角形的概念性质及两个全等三角形全等的条件等解决问题，会利用角平分线及线段垂直平分线的概念、性质解决问题。

1、　 知道补角、余角、对顶角、同位角、内错角、同旁内角的概念，能根据图形或数量关系判断两个角之间的关系，知道三角形三边之间的关系、三角形的内角和定理及三角形的内角、外角、中线、高、角平分线等概念；知道平行线的概念及性质及两直线平行的条件；知道全等三角形的概念、性质及三角形全等的条件；知道角平分线、线段垂直平分线的概念及性质。

1、　 师自行设计作业。2、复习指导用书P61-63。

第13课时 平行线、三角形与证明

溧阳市第二中学 朱淑芳

复习教学目标：

2．　 本节课运用的数学思想方法：类比思想、数形结合思想、分类思想等。

Ⅳ. [实践]

1．　 本单元知识结构(见填空第1题)。