5、　 会求多边形的内角和，并能判定一个多边形是几边形；会进行有关平行四边形的边角的简单计算；能运用性质和判定进行相关的证明；能识别中心对称图形。

4、　 能说出多边形的内角和定理和外角和定理；知道平行四边形的性质和判断；

2、　 分类讨论的思想、(如：在等腰三角形中，若已知一个角求另外两个角或已知一边求另外两边，通常要分类讨论)、数形结合的思想，转化的思想等。

Ⅳ、[实践]

(1)　　　 教师自行设计作业；

(2)　　　 复习指导用书第83--86页第1、3、4、9、13、14、19、22、25、26题。

第15课时　 多边形、平行四边形和证明

溧阳市第二中学　　 彭云

复习教学目标:

1、　 本节课主要内容：见唤醒中的“知识结构图”。

5、直角三角形斜边上的中线和面积分别是5 cm　 ，20 cm²，则它的斜边上的高是　 (　 )

　 A、3 cm　　　 B、4 cm　　　　 C、5 cm　　　 　D、2

Ⅱ、[尝试]

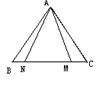例1:已知，在△ABC中，AB=AC，点M，N在BC上，且AM=AN，请你用最简便的方法说明BM=CN 。

分析：作底边上的高，灵活运用“三线合一”性质

证明：略

提炼：究竟作角平分线还是作高或中线，要依具体问题。

例2、已知:如图,在△ABC中,D是BC边上的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC

(提示:先用“HL”证△BDE≌△DFC,然后运用“等角对等边”得证)

证明：略

提炼:在直角三角形中会灵活运用“HL”定理

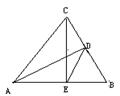例3:如图，已知在△ABC中，AD、CE是高，且AE=3，BE=2，CE=4，在不添加任何辅助线和字母的条件下，你能得到哪些正确结论？(分别从边、角、三角形相似三个角度去思考)

分析：首先从高和一些线段的长的角度去思考，由直角三角形中的边联想到运　　　 用勾股定理求出AC、AD、BC、DE，然后利用等腰三角形、直角三角形，三角形相似等有关知识逐步得到结论。

解：①AB=AC，②BD=CD=DE，③AD=BC，④∠ABC=∠ACB=∠BED，⑤∠BDE∠=BAC，　　　 ⑥∠BAD=∠CAD=∠BCE=∠CED，⑦∠ACE=∠ADE，⑧∠ACD+∠ AED=180°， ∠BAC+∠CDE=180°，⑨△BAD≌△CAD，⑩△BAD∽△BCE，⑾△CAD∽△BCE，⑿△BDE∽△BAC

提炼：注意仔细分析已知条件，思考哪些已知条件组合在一起可以产生新的结论及可能产生的新的结论。

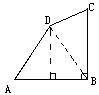
例4:如图，在四边形ABCD中，AB=AD=4，∠A=60°，∠D=150°,CB⊥AB，已知四边形ABCD的周长为16，求S_{四边形ABCD}

分析：不规则图形往往转化为规则图形，若连接BD后，由AB=AD=4，∠A=60°容

易判断△BAD是等边三角形，并且得到△BDC是含30°角的直角三角形，那么S_{四边形ABCD}=S _△ABD+S_△CBD，根据已知条件可算到CD+BC=8，然后根据2CD=BC可求出CD,BC。

解：　 连接BD，则△BAD为等边三角形，∴AD= BD=4，∠ADB=60°，CD+BC=8

又∠ADC=150°，∴∠BDC=90°,∠DBC=30°

在Rt△BDC中可求得CD=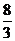,BC=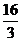,BD=BC*cos30°=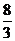

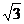
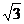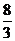
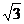∴S_{四边形ABCD}= S _△ABD+S_△CBD=×4×2+×4×=4+=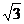

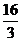
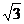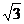
提炼：运用“转化”的数学思想将不规则图形转化为规则图形，注意在等边三角形和直角三角形中运用其性质灵活求解三角形的边长。

变式: 在四边形ABCD中，AB=AD=4，∠A=60°，∠D=150°,四边形ABCD的周长为16，又该如何求

S_{四边形ABCD}?

分析:注意在直角三角形中常用勾股定理建立方程求边长。

如:设CD=x，则BC=16-4-4-x=8-x

在BDC中，有BC²=BD²+DC²，即(8-x)²=x²+4²，解得x=3。∴CD=3,BC=5.(略)　　　　　　　　

Ⅲ、[小结]

4、等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为　　 (　　 )

　 A、75°或15°　　 B、30°或60°　　 C、75°　　　 D、30°

3、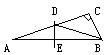如图，在Rt△ABC中，斜边AB的垂直平分线分别交AB、AC于点E、D，∠A=15°，若AD=4，则BC=　　　　　　　　　　 　　　　　　(　　 )

A、4　　　　 B、2　　　 C、1　　 D、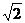

2、已知一个直角三角形的两边长分别是3和4，则第三边的长是(　 )

A、4　　　　 B、5　　　　 C、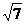　　 D、5或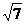

1、等腰三角形的一边长是10cm，另一边长是6 cm，则它的周长是　 　(　　 )

A、26 cm　　　　 B、22 cm　　　 C、16 cm　　　 D、22 cm或26 cm

6、有两边对应相等的直角三角形是全等三角形.(　　 )