
(1)教师自行设计作业 (2)复习指导:14页第3题单数、17页3、4
 第5课时
一次方程
分式方程
一次方程组
第5课时
一次方程
分式方程
一次方程组
燕山中学 居群芳
复习教学目标
1、了解一次方程、分式方程、二元一次方程组的概念。知道方程组的解的含义。理解分式方程产生增根的原因。理解二元一次方程与一次函数的关系。说出解整式方程和分式方程的异同,
2、 这节课复习因式分解的应用,化简分式。在化简分式时,注意的运算顺序和符号,防止出错。其次比较两个代数式值的大小可以用作差法。
1、 带领学生回顾尝试中的填空题。
例1有这样的一道题:“计算: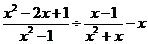 的值,其中x=2006。”甲同学把
的值,其中x=2006。”甲同学把
“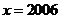 ”错抄成“
”错抄成“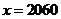 ”,但他的计算结果也是正确的。你说这是怎么回事?
”,但他的计算结果也是正确的。你说这是怎么回事?
解 原式=0 因为化简结果不含x,所以无论他抄什么值,结果都是正确的。
提炼:如果把x的值抄错,而不影响计算结果,这一类题的化简结果一定是一个常数,与x的取值无关;
如果把x的值抄成它的相反数,而不影响计算结果,这一类题的化简结果一定是一个常数或者是
关于x偶次幂的代数式,与x的符号无关。
例2 化简
(1)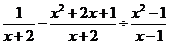 (2)(
(2)(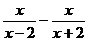 )
)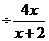
解 (1)原式=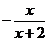 (2)原式=
(2)原式=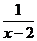
提炼:(1) 解题时要注意分式的运算顺序,先乘除,再加减,有括号优先,其次能分解的多项式要分解因式,便于约分,结果一定要是最简分式。
(2)对于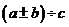 分配律仍适用,但
分配律仍适用,但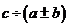 不能用分配律。
不能用分配律。
例3 已知: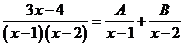 ,求整式A、B。
,求整式A、B。
分析:由于要求A、B,等式的左边是已知,右边是未知,可以从未知化到已知。故把等式作恒等变形,得到等式左右两边分母相同,所以分子也相同,转化为关于A、B的一个二元一次方程组,再求解。
解 A=1 B=2
提炼:本例是分式运算的逆向运用,两个代数式恒等,首先是化结构相同,其次是利用相同项的系数也相同求未知量。
例4 甲、乙两人进行百米赛跑,甲前半程的速度为m米/秒,后半程的速度为n米/秒;乙前半时的速度为m米/秒,后半时的速度为n米/秒。问:谁先到达终点?
分析:本题首先要用m、n的代数式表示甲、乙两人到达终点的时间t1、t2,比较t1、t2的大小,可以转化为t1-t2与0比较
解 见复习指导用书第16页
提炼:(1)比较两个代数式A、B的值的大小,通常可用作差的方法,当A-B﹥0,则A﹥B;当A-B=0,则A=B;当A-B﹤0,则A﹤B。
(2)由于本例中没有指明m、n的大小,所以要分m=n与m≠n两种情况讨论。
3、选择题
(1)若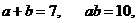 则
则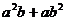 的值应是
( C )
的值应是
( C )
A.7 B.10 C.70 D.17
(2)下列各式分解不正确的是 ( C )
A、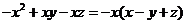 B、
B、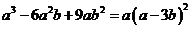
C、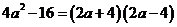 D、
D、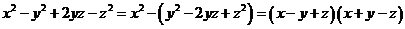
(3)分解因式: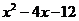 的结果是
( C )
的结果是
( C )
A、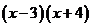 B、
B、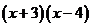 C、
C、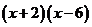 D、
D、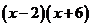
(4)下列等式成立的是 ( D )
A 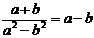 B
B 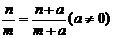 C
C 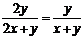 D
D 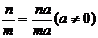
(5)化简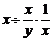 等于
( C )A 1
B
等于
( C )A 1
B 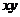 C
C
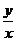 D
D 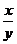
2、判断题
(1)等式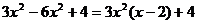 从左到右的变形是分解因式
( × )
从左到右的变形是分解因式
( × )
(2)只要分式的分子为零,则分式的值就为零 ( × )
(3)分式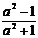 有意义,则a≠±1
( × )
有意义,则a≠±1
( × )
1、填空题
 (1)
(1)
(2)因式分解中的公式有 , ,
(3)分式的乘(除)法法则是 ,
分式的加(减)法法则是 ,
3、会逆用乘法公式、乘法法则验证因式分解;会用类比的方法得出分式的性质和运算法则;会用作差法比较两个代数式值的大小。
复习教学过程设计
2、 会灵活应用四种方法进行因式分解;会利用分式基本性质进行约分和通分;会进行简单的分式加、减、乘、除运算。
1、 知道因式分解、分式的概念;能说出分式的基本性质。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com