
2. 复习指导用书第9页第3、7、8题和第12页第3题。
第4课时 因式分解 分式
燕山中学 王爱军
复习教学目标
1. 教师自行设计作业。
2. 本节课运用的数学思想方法:类比思想,一般到特殊、再由特殊到一般的思想方法和数形结合思想等。
Ⅳ. [实践]
1. 本单元的知识结构(见填空)。
5.  ( )
( )
A. 4 B. 8 C. 4 或-4 D. 8或-8
Ⅱ. [尝试]
例1.先化简,再求值: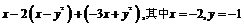 。 (答案:11)
。 (答案:11)
例2.计算: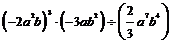
分析:按整式混合运算的顺序:先乘方,同级运算从左往右依次进行。(答案:36b)
提炼:在熟练掌握整式的运算法则和幂的运算性质基础上必须严格按照混合运算顺序逐步运算。
例3.计算:(1) ; (2)
; (2)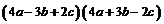
分析:第(1)题根据混合运算法则先合理使用乘法公式,后进行整式的加减运算。
第(2)题先将原式转化为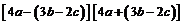 的形式,后运用平方差公式将其化为
的形式,后运用平方差公式将其化为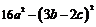 的形式,最后利用完全平方公式计算即可。(答案见复习指导用书第11页)
的形式,最后利用完全平方公式计算即可。(答案见复习指导用书第11页)
提炼:根据乘法公式的特点将原题中的代数式变形为符合公式特点的形式是解此类题的关键。
例4. 见《复习指导用书》第6页例2
分析:解决本题时学生往往着眼于分析表格中的数据的变化,应指导学生结合具体的图形观察图形的形成规律,着重在摆成的平行四边形的两组对边与菱形和等腰梯形的边长之间的关系。
提炼:本例是一道探索题,首先给出了几个特殊的图形,然后根据这些特殊的图形的周长,进行探索、归纳、猜想,得到一般图形的周长,体现了数学中常见的由一般到特殊、再由一般到特殊的思想方法以及数形结合思想。
Ⅲ. [小结]
4.下列各式中,不能用平方差公式计算的是 ( )
A. 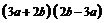 B.
B. 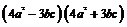 C.
C.  D.
D. 
3.下列各式计算过程正确的是 ( )
A. 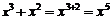 B.
B. 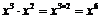 C.
C. 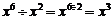 D.
D. 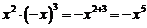
2.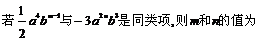 ( )
( )
A. 4和3 B. 2和3 C . 4 和2 D. 无法确定
1.某商场实行7.5折优惠销售,现售价为y元的商品的原价为 ( )
A. 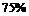 y 元 B.
y 元 B. 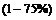 y元 C .
y元 C . 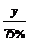 元
D.
元
D. 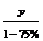 元
元
5. 。
( )
。
( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com