
7.(09常德)给你一只标有“10Ω 0.3A”的定值电阻和一只标有“30Ω 0.6A”的滑动变阻器,在保证所有电路元件安全的前提下,若串联接入电路,则电路中允许通过的最大电流为 A,它们两端允许加的最大电压为 V。
答案:0.3A 12V
6.(09常德)如图所示电路中,电源电压保持不变,当开关S闭合,滑动变阻器的滑片P向右移动时,电表的示数变化情况是C
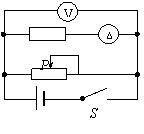 A.电流表示数增大,电压表示数增大
A.电流表示数增大,电压表示数增大
B.电流表示数减小,电压表示数增大
C.电流表示数不变,电压表示数不变
D.电流表示数减小,电压表示数不变
5.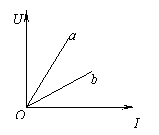 (09常德)某同学在探究“电阻上的电流跟两端电压的关系”时,发现通过电阻a、b的电流随电压变化情况如图所示,则下列结论与图象相符的是D
(09常德)某同学在探究“电阻上的电流跟两端电压的关系”时,发现通过电阻a、b的电流随电压变化情况如图所示,则下列结论与图象相符的是D
A.电阻一定时,电流随着电压的增大而减小
B.电压相同时,阻值大的电阻通过的电流大
C.电流相同时,阻值小的电阻两端的电压大
D.两电阻阻值的关系是Ra>Rb
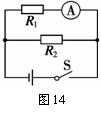
4.(09福州)(4分)在图14电路中,R1=10Ω,R2=20Ω,闭合开关后,电流表
的示数为0.3A。
(1)电阻R1两端的电压是多少?(2)通过R2的电流是多少?
答案:3V 0.15A。
3.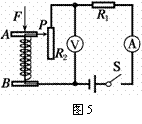 (09福州)如图5所示是童童设计的压力传感器的原理图,
(09福州)如图5所示是童童设计的压力传感器的原理图,
其中弹簧上端和滑动变阻器的滑片P固定在一起,AB间有可
收缩的导线,R1为定值电阻。当闭合开关S,压力F增大时,
电流表与电压表示数变化情况是B
A.电流表示数变大,电压表示数变小
B.电流表示数变小,电压表示数变大
C.电流表、电压表示数都变大
 D.电流表、电压表示数都变小
D.电流表、电压表示数都变小
1.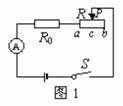 (2009年安顺市)如图l 所示,设电源电压保持不变,R0=10W。当闭合开关S,滑动变阻器的滑片P在中点c 时,电流表的示数为0.3A ,移动滑片P至b 端时,电流表的示数为0.2A .则电源电压U 与滑动变阻器的最大阻值R分别为:B
(2009年安顺市)如图l 所示,设电源电压保持不变,R0=10W。当闭合开关S,滑动变阻器的滑片P在中点c 时,电流表的示数为0.3A ,移动滑片P至b 端时,电流表的示数为0.2A .则电源电压U 与滑动变阻器的最大阻值R分别为:B
A.U = 3V,R = 5W;
B.U = 6V,R=20W;
C.U = 6V,R = 10W;
D.U = 3V,R = 15W。
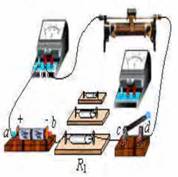 2(6分)(2009年安顺市)刘阳同学想利用图8 所给实验器材,探究电流与电压和电阻的关系。
2(6分)(2009年安顺市)刘阳同学想利用图8 所给实验器材,探究电流与电压和电阻的关系。
|
实验次数 |
1 |
2 |
3 |
4 |
5 |
|
电压/V |
l.0 |
1.5 |
2.0 |
2.5 |
2.8 |
|
电流/A |
0.10 |
0.l5 |
0.20 |
0.25 |
0.28 |
(1)在电压表尚未接入电路之前,已存在两处明显的连接错误,请你指出。
(2)假如错误已纠正,且原电流方向不变,则电压表将接在电路中a、b、c、d四点中的哪两点才能测量R1两端的电压。
(3)上表是刘阳同学用R1实验得出的几组实验数据,分析表中数据可得到什么结论?写出简要的分析过程。
(4)本实验操作完成后,如果将电阻R1换成一只小灯泡,还能测量小灯泡的什么物理量?
答案(1)电流表正负接线错误,滑动变阻器接线错误(其它合理的表述即可)。…(2分)
(2)bc(或bd) ………………………………………………………………(1分)
(3)电阻一定时,导体中的电流与它两端的电压成正比。……………………(1分)
当电压增加时,电流也随着增加,且电压与电流的比值不变(其它合理的表述即可)。…(1分)
(4)电功率、电阻 ………………………………………………………………(1分)
20.(天津19)(本小题满分12分)
如图,在五面体ABCDEF中,FA  平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE= AD
AD
(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
本小题要考查异面直线所成的角、平面与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想像能力、运算能力和推理论证能力。满分12分.
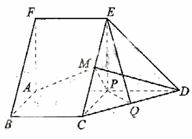 方法一:(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其补角)为异面直线BF与DE所成的角。设P为AD的中点,连结EP,PC。因为FE
方法一:(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其补角)为异面直线BF与DE所成的角。设P为AD的中点,连结EP,PC。因为FE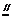 AP,所以FA
AP,所以FA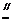 EP,同理AB
EP,同理AB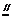 PC。又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=
PC。又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=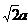 ,故∠CED=60°。所以异面直线BF与DE所成的角的大小为60°
,故∠CED=60°。所以异面直线BF与DE所成的角的大小为60°
(II)证明:因为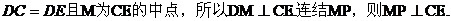
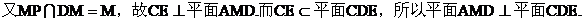 (III)
(III)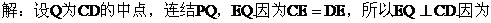
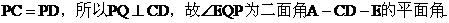
由(I)可得,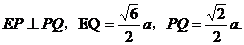
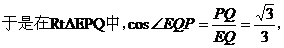
方法二:如图所示,建立空间直角坐标系,
点 为坐标原点。设
为坐标原点。设 依题意得
依题意得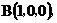
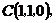
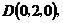
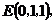
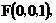
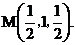
(I)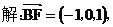
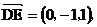
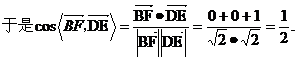
所以异面直线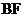 与
与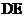 所成的角的大小为
所成的角的大小为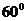 .
.
(II)证明: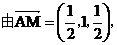
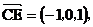
 ,
,
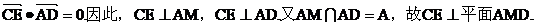
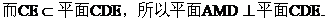
(III)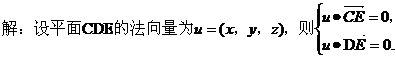

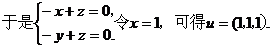
又由题设,平面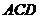 的一个法向量为
的一个法向量为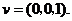
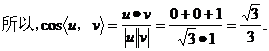
19.(江苏16)(本小题满分14分)
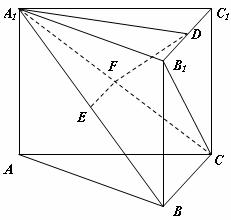 如图,在直三棱柱
如图,在直三棱柱 中,
中,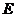 、
、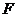 分别是
分别是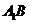 、
、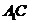 的中点,点
的中点,点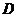 在
在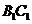 上,
上,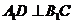 。
。
求证:(1)EF∥平面ABC;
(2)平面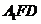
 平面
平面 .
.
 [解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查空间想象能力、推理论证能力。满分14分。
[解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查空间想象能力、推理论证能力。满分14分。

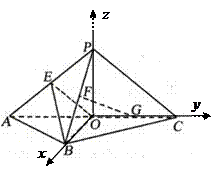
18.(浙江
|
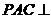 平面
平面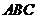 ,
,
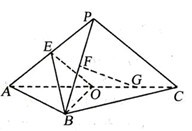 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为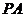 ,
,
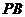 ,
,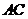 的中点,
的中点,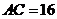 ,
,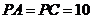 .
.
(I)设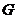 是
是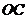 的中点,证明:
的中点,证明: 平面
平面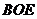 ;
;
(II)证明:在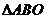 内存在一点
内存在一点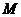 ,使
,使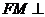 平面
平面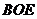 ,并求点
,并求点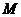 到
到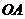 ,
,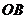 的距离.
的距离.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为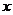 轴,
轴, 轴,
轴,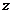 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O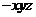 ,
,
 则
则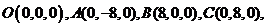
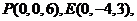
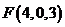 ,由题意得,
,由题意得,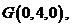 因
因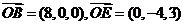 ,因此平面BOE的法向量为
,因此平面BOE的法向量为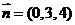 ,
,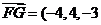 得
得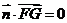 ,又直线
,又直线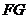 不在平面
不在平面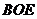 内,因此有
内,因此有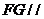 平面
平面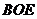
(II)设点M的坐标为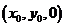 ,则
,则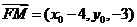 ,因为
,因为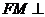 平面BOE,所以有
平面BOE,所以有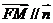 ,因此有
,因此有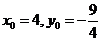 ,即点M的坐标为
,即点M的坐标为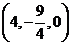 ,在平面直角坐标系
,在平面直角坐标系 中,
中, 的内部区域满足不等式组
的内部区域满足不等式组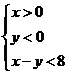 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在 内存在一点
内存在一点 ,使
,使 平面
平面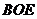 ,由点M的坐标得点
,由点M的坐标得点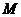 到
到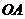 ,
,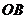 的距离为
的距离为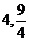 .
.
17.(山东18)(本小题满分12分)
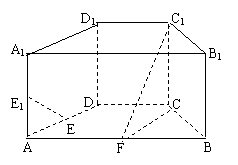 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA =2, E、E
=2, E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
(1)
证明:直线EE //平面FCC
//平面FCC ;
;
(2)
求二面角B-FC -C的余弦值。
-C的余弦值。 

解法一:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
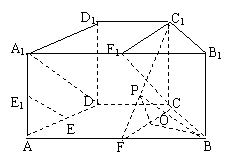 连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为 平面FCC
平面FCC ,
,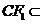 平面FCC
平面FCC ,
,
所以直线EE //平面FCC
//平面FCC .
.
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A B
B C
C D
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,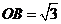 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵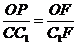 ∴
∴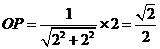 ,
, 

在Rt△OPF中,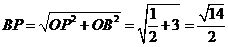 ,
,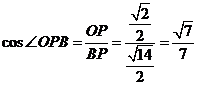 ,所以二面角B-FC
,所以二面角B-FC -C的余弦值为
-C的余弦值为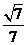 .
.
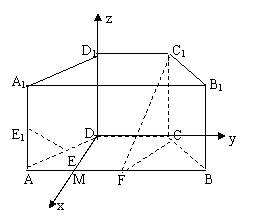 解法二:(1)因为AB=4, BC=CD=2,
F是棱AB的中点,
解法二:(1)因为AB=4, BC=CD=2,
F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
,则D(0,0,0),A(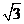 ,-1,0),F(
,-1,0),F(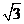 ,1,0),C(0,2,0),
,1,0),C(0,2,0),
C1(0,2,2),E(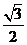 ,
,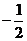 ,0),E1(
,0),E1(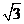 ,-1,1),所以
,-1,1),所以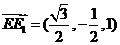 ,
,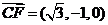 ,
,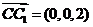
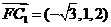 设平面CC1F的法向量为
设平面CC1F的法向量为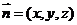 则
则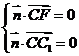 所以
所以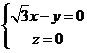 取
取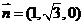 ,则
,则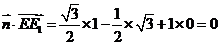 ,所以
,所以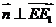 ,所以直线EE
,所以直线EE //平面FCC
//平面FCC .
. 

(2)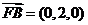 ,设平面BFC1的法向量为
,设平面BFC1的法向量为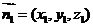 ,则
,则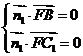 所以
所以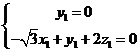 ,取
,取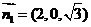 ,则
,则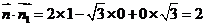 ,
,
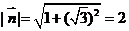 ,
,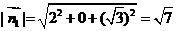 ,
, 

所以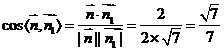 ,由图可知二面角B-FC
,由图可知二面角B-FC -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC -C的余弦值为
-C的余弦值为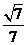 .
. 

[命题立意]:本题主要考查直棱柱的概念、线面位置关系的判定和二面角的计算.考查空间想象能力和推理运算能力,以及应用向量知识解答问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com