
题型1:柱体的体积和表面积
例1.一个长方体全面积是20cm2,所有棱长的和是24cm,求长方体的对角线长.
解:设长方体的长、宽、高、对角线长分别为xcm、ycm、zcm、lcm
依题意得: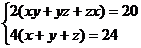
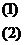
由(2)2得:x2+y2+z2+2xy+2yz+2xz=36(3)
2.旋转体的面积和体积公式
|
名称 |
圆柱 |
圆锥 |
圆台 |
球 |
|
S侧 |
2πrl |
πrl |
π(r1+r2)l |
|
|
S全 |
2πr(l+r) |
πr(l+r) |
π(r1+r2)l+π(r21+r22) |
4πR2 |
|
V |
πr2h(即πr2l) |
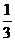 πr2h πr2h |
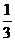 πh(r21+r1r2+r22) πh(r21+r1r2+r22) |
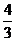 πR3 πR3 |
表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台 上、下底面半径,R表示半径。
1.多面体的面积和体积公式
|
名称 |
侧面积(S侧) |
全面积(S全) |
体
积(V) |
|
|
棱 柱 |
棱柱 |
直截面周长×l |
S侧+2S底 |
S底·h=S直截面·h |
|
直棱柱 |
ch |
S底·h |
||
|
棱 锥 |
棱锥 |
各侧面积之和 |
S侧+S底 |
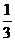 S底·h S底·h |
|
正棱锥 |
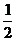 ch′ ch′ |
|||
|
棱 台 |
棱台 |
各侧面面积之和 |
S侧+S上底+S下底 |
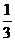 h(S上底+S下底+ h(S上底+S下底+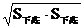 ) ) |
|
正棱台 |
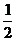 (c+c′)h′ (c+c′)h′ |
表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。即使考查空间线面的位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解。
由于本讲公式多反映在考题上,预测008年高考有以下特色:
(1)用选择、填空题考查本章的基本性质和求积公式;
(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;
了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
4.画水平放置的多边形的直观图的关键是确定多边形顶点的位置,因为多边形顶点的位置一旦确定,依次连结这些顶点就可画出多边形来,因此平面多边形水平放置时,直观图的画法可以归结为确定点的位置的画法。强调斜二测画法的步骤。
3.
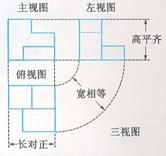 三视图画法规则
三视图画法规则
高平齐:主视图与左视图的高要保持平齐
长对正:主视图与俯视图的长应对正
宽相等:俯视图与左视图的宽度应相等
2.一些特殊棱柱、棱锥、棱台的概念和主要性质
|
名称 |
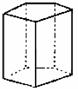
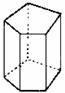
棱柱 |
直棱柱 |
正棱柱 |
|
图 形 |
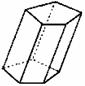 |
 |
 |
|
定 义 |
有两个面互相平行,而其余每相邻两个面的交线都互相平行的多面体 |
侧棱垂直于底面的棱柱 |
底面是正多边形的直棱柱 |
|
侧棱 |
平行且相等 |
平行且相等 |
平行且相等 |
|
侧面的形状 |
平行四边形 |
矩形 |
全等的矩形 |
|
对角面的形状 |
平行四边形 |
矩形 |
矩形 |
|
平行于底面的截面的形状 |
与底面全等的多边形 |
与底面全等的多边形 |
与底面全等的正多边形 |
|
名称 |
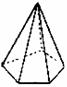
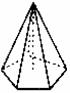
棱锥 |
正棱锥 |
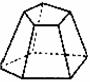
棱台 |
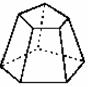
正棱台 |
|
图形 |
 |
 |
 |
 |
|
定义 |
有一个面是多边形,其余各面是有一个公共顶点的三角形的多面体 |
底面是正多边形,且顶点在底面的射影是底面的射影是底面和截面之间的部分 |
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分 |
由正棱锥截得的棱台 |
|
侧棱 |
相交于一点但不一定相等 |
相交于一点且相等 |
延长线交于一点 |
相等且延长线交于一点 |
|
侧面的形状 |
三角形 |
全等的等腰三角形 |
梯形 |
全等的等腰梯形 |
|
对角面的形状 |
三角形 |
等腰三角形 |
梯形 |
等腰梯形 |
|
平行于底的截面形状 |
与底面相似的多边形 |
与底面相似的正多边形 |
与底面相似的多边形 |
与底面相似的正多边形 |
|
其他性质 |
|
高过底面中心;侧棱与底面、侧面与底面、相邻两侧面所成角都相等 |
|
两底中心连线即高;侧棱与底面、侧面与底面、相邻两侧面所成角都相等 |
几种特殊四棱柱的特殊性质
|
名称 |
特殊性质 |
|
平行六面体 |
底面和侧面都是平行四边行;四条对角线交于一点,且被该点平分 |
|
直平行六面体 |
侧棱垂直于底面,各侧面都是矩形;四条对角线交于一点,且被该点平分 |
|
长方体 |
底面和侧面都是矩形;四条对角线相等,交于一点,且被该点平分 |
|
正方体 |
棱长都相等,各面都是正方形四条对角线相等,交于一点,且被该点平分 |
1.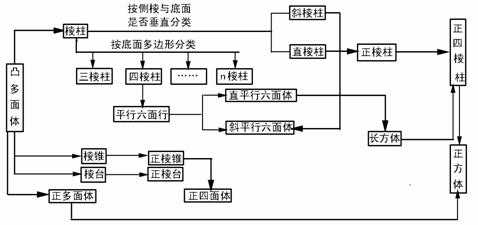 几种常凸多面体间的关系
几种常凸多面体间的关系
题型1:空间几何体的构造
例1.(1)(06北京理4)平面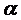 的斜线 AB 交
的斜线 AB 交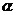 于点 B,过定点 A 的动直线
于点 B,过定点 A 的动直线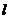 与 AB 垂直,且交
与 AB 垂直,且交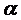 于点 C,则动点C的轨迹是( )
于点 C,则动点C的轨迹是( )
A.一条直线 B.一个圆 C.一个椭圆 D.双曲线的一支
(2)(04天津文 8)如图,定点A和B都在平面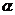 内,定点
内,定点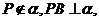 C是
C是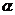 内异于A和B的动点,且
内异于A和B的动点,且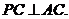 那么,动点在平面
那么,动点在平面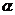 内的轨迹是( )
内的轨迹是( )
A.一条线段,但要去掉两个点 B.一个圆,但要去掉两个点
C.一个椭圆,但要去掉两个点 D.半圆,但要去掉两个点
(3)正方体ABCD_A1B1C1D1的棱长为2,点M是BC的中点,点P是平面ABCD内的一个动点,且满足PM=2,P到直线A1D1的距离为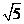 ,则点P的轨迹是[ ]
,则点P的轨迹是[ ]
A.圆 B.双曲线 C.两个点 D.直线
解析:(1)设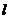 与
与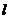 ¢是其中的两条任意的直线,则这两条直线确定一个平面,且斜线
¢是其中的两条任意的直线,则这两条直线确定一个平面,且斜线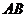 垂直这个平面,由过平面外一点有且只有一个平面与已知直线垂直可知过定点
垂直这个平面,由过平面外一点有且只有一个平面与已知直线垂直可知过定点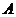 与
与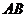 垂直所有直线都在这个平面内,故动点C都在这个平面与平面
垂直所有直线都在这个平面内,故动点C都在这个平面与平面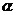 的交线上,故选A。
的交线上,故选A。
(2)答案为B。
(3)解析: 点P到A1D1的距离为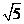 ,则点P到AD的距离为1,满足此条件的P的轨迹是到直线AD的距离为1的两条平行直线,
,则点P到AD的距离为1,满足此条件的P的轨迹是到直线AD的距离为1的两条平行直线,
又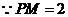 ,
,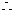 满足此条件的P的轨迹是以M为圆心,半径为2的圆,这两种轨迹只有两个交点.
满足此条件的P的轨迹是以M为圆心,半径为2的圆,这两种轨迹只有两个交点.
故点P的轨迹是两个点。选项为C。
点评:该题考察空间内平面轨迹的形成过程,考察了空间想象能力。
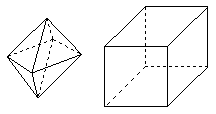 例2.(06江苏9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )
例2.(06江苏9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )
A.1个 B.2个 C.3个 D.无穷多个
解析:由于两个正四棱锥相同,所以所求几何体的中心在正四棱锥底面正方形ABCD中心,有对称性知正四棱锥的高为正方体棱长的一半,影响几何体体积的只能是正四棱锥底面正方形ABCD的面积,问题转化为边长为1的正方形的内接正方形有多少种,所以选D。
点评:本题主要考查空间想象能力,以及正四棱锥的体积。正方体是大家熟悉的几何体,它的一些内接或外接图形需要一定的空间想象能力,要学会将空间问题向平面问题转化。
题型2:空间几何体的定义
例3.(06江西文9)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是( B )
A.等腰四棱锥的腰与底面所成的角都相等
B.等腰四棱锥的侧面与底面所成的二面角都相等或互补
C.等腰四棱锥的底面四边形必存在外接圆
D.等腰四棱锥的各顶点必在同一球面上
解析:因为“等腰四棱锥”的四条侧棱都相等,所以它的顶点在底面的射影到底面的四个顶点的距离相等,故A,C正确,且在它的高上必能找到一点到各个顶点的距离相等,故D正确,B不正确,如底面是一个等腰梯形时结论就不成立。故选B
点评:抓住本质的东西来进行判断,对于信息要进行加工再利用。
例4.(2002北京理,10)设命题甲:“直四棱柱ABCD-A1B1C1D1中,平面ACB1与对角面BB1D1D垂直”;命题乙:“直四棱柱ABCD-A1B1C1D1是正方体”.那么,甲是乙的( )
A.充分必要条件
B.充分非必要条件
C.必要非充分条件
D.既非充分又非必要条件C
解析:若命题甲成立,命题乙不一定成立,如底面为菱形时。若命题乙成立,命题甲一定成立。答案为C。
点评:对于空间几何体的定义要有深刻的认识,掌握它们并能判断它们的性质。
题型3:空间几何体中的想象能力
例5.(2002上海春,10)图9-12表示一个正方体表面的一种展开图,图中的四条线段AB、CD、EF和GH在原正方体中相互异面的有 对.
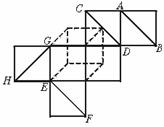
解析:相互异面的线段有AB与CD,EF与GH,AB与GH3对.
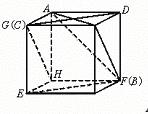
点评:解决此类题目的关键是将平面图形恢复成空间图形,较强的考察了空间想象能力。
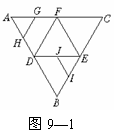 例6.(2003京春文11,理8)如图9-1,在正三角形ABC中,D,E,F分别为各边的中点,G,H,I,J分别为AF,AD,BE,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度数为( )
例6.(2003京春文11,理8)如图9-1,在正三角形ABC中,D,E,F分别为各边的中点,G,H,I,J分别为AF,AD,BE,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度数为( )
A.90° B.60°
C.45° D.0°
答案:B
解析:将三角形折成三棱锥如图9-43所示.HG与IJ为一对异面直线.过点D分别作HG与IJ的平行线,即DF与AD.所以∠ADF即为所求.因此,HG与IJ所成角为60°。
点评:在画图过程中正确理解已知图形的关系是关键。通过识图、想图、画图的角度考查了空间想象能力。而对空间图形的处理能力是空间想象力深化的标志,是高考从深层上考查空间想象能力的主要方向。
题型4:斜二测画法
例7.画正五棱柱的直观图,使底面边长为3cm侧棱长为5cm。
解析:先作底面正五边形的直观图,再沿平行于Z轴方向平移即可得。
作法:
(1)画轴:画X′,Y′,Z′轴,使∠X′O′Y′=45°(或135°),∠X′O′Z′=90°。
(2)画底面:按X′轴,Y′轴画正五边形的直观图ABCDE。
(3)画侧棱:过A、B、C、D、E各点分别作Z′轴的平行线,并在这些平行线上分别截取AA′,BB′,CC′,DD′,EE。′
(4)成图:顺次连结A′,B′,C′,D′,F′,加以整理,去掉辅助线,改被遮挡的部分为虚线。
点评:用此方法可以依次画出棱锥、棱柱、棱台等多面体的直观图。
例8.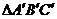 是正△ABC的斜二测画法的水平放置图形的直观图,若
是正△ABC的斜二测画法的水平放置图形的直观图,若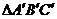 的面积为
的面积为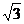 ,那么△ABC的面积为_______________。
,那么△ABC的面积为_______________。
解析: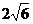 。
。
点评:该题属于斜二测画法的应用,解题的关键在于建立实物图元素与直观图元素之间的对应关系。特别底和高的对应关系。
题型5:平行投影与中心投影
例9.(1)如图,在正四面体A-BCD中,E、F、G分别是三角形ADC、ABD、BCD的中心,则△EFG在该正四面体各个面上的射影所有可能的序号是( )
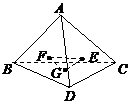
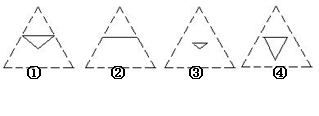
A.①③ B.②③④ C.③④ D.②④
(2)(2000全国,16)如图9-15(1),E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是图9-15(2)的 (要求:把可能的图的序号都填上).
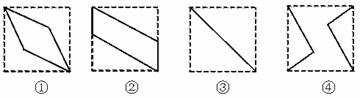
解析:(1)正四面体各面的中点在四个面上的射影不可能落到正四面体的边上,所以①②不正确,根据射影的性质E、F、G、三点在平面ABC内的射影形状如“④”所示,在其它平面上的射影如“③”所示。答案:C;
(2)答案:②③;解析:∵面BFD1E⊥面ADD1A1,所以四边形BFD1E在面ADD1A1上的射影是③,同理,在面BCC1B1上的射影也是③。过E、F分别作DD1和CC1的垂线,可得四边形BFD1E在面DCC1D1上的射影是②,同理在面ABB1A1,面ABCD和面A1B1C1D1上的射影也是②。
点评:考查知识立足课本,对空间想象能力、分析问题的能力、操作能力和思维的灵活性等方面要求较高,体现了加强能力考查的方向。
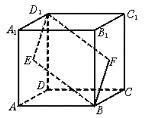
例10.(06 安徽理16)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面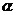 内,其余顶点在
内,其余顶点在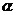 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到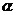 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面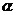 的距离可能是: ①3; ②4; ③5; ④6; ⑤7
的距离可能是: ①3; ②4; ③5; ④6; ⑤7
以上结论正确的为________________________(写出所有正确结论的编号)
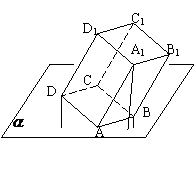 解析:如图,B、D、A1到平面
解析:如图,B、D、A1到平面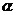 的距离分别为1、2、4,则D、A1的中点到平面
的距离分别为1、2、4,则D、A1的中点到平面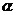 的距离为3,所以D1到平面
的距离为3,所以D1到平面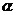 的距离为6;B、A1的中点到平面
的距离为6;B、A1的中点到平面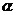 的距离为
的距离为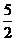 ,所以B1到平面
,所以B1到平面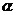 的距离为5;则D、B的中点到平面
的距离为5;则D、B的中点到平面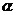 的距离为
的距离为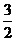 ,所以C到平面
,所以C到平面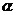 的距离为3;C、A1的中点到平面
的距离为3;C、A1的中点到平面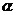 的距离为
的距离为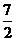 ,所以C1到平面
,所以C1到平面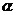 的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
点评:该题将计算蕴涵于射影知识中,属于难得的综合题目。
题型6:三视图
例11.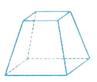 (1)画出下列几何体的三视图
(1)画出下列几何体的三视图
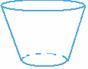
|
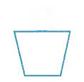
 解析:这二个几何体的三视图如下
解析:这二个几何体的三视图如下
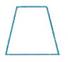
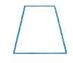


(2)如图,设所给的方向为物体的正前方,试画出它的三视图(单位:cm)
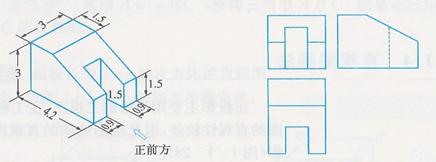
点评:画三视图之前,应把几何体的结构弄清楚,选择一个合适的主视方向。一般先画主视图,其次画俯视图,最后画左视图。画的时候把轮廓线要画出来,被遮住的轮廓线要画成虚线。物体上每一组成部分的三视图都应符合三条投射规律。
例12.某物体的三视图如下,试判断该几何体的形状
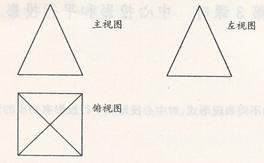
解析:该几何体为一个正四棱锥分析:三视图是从三个不同的方向看同一物体得到的三个视图。
点评:主视图反映物体的主要形状特征,主要体现物体的长和高,不反映物体的宽。而俯视图和主视图共同反映物体的长要相等。左视图和 俯视图共同反映物体的宽要相等。据此就不难得出该几何体的形状。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com