
11.(2009浙江文)设等比数列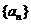 的公比
的公比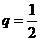 ,前
,前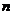 项和为
项和为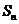 ,则
,则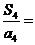 .
.
1.(2009年广东卷文)已知等比数列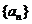 的公比为正数且
的公比为正数且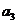 ·
· =2
=2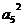
 =1则
=1则 = A
= A B
B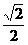 C
C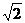 D.2
D.2
5.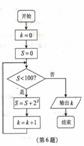 (浙江文6)某程序框图如图所示,该程序运行后输出的k的值是A4
B5C6D7
(浙江文6)某程序框图如图所示,该程序运行后输出的k的值是A4
B5C6D7
数列部分
17.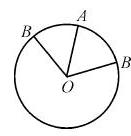 (2009福建卷文)点A为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B,则劣弧
(2009福建卷文)点A为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B,则劣弧 AB的长度小于1的概率为 。
AB的长度小于1的概率为 。
算法部分
14.(2009江苏卷)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
|
学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲班 |
6 |
7 |
7 |
8 |
7 |
|
乙班 |
6 |
7 |
6 |
7 |
9 |
则以上两组数据的方差中较小的一个为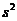 = .
= . 
13.(2009江苏卷)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 .
12.(2009安徽卷文)从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是________。
3.(2009山东卷文)在区间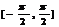 上随机取一个数x,cosx的值介于0到
上随机取一个数x,cosx的值介于0到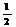 之间的概率为( ).A.
之间的概率为( ).A.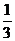 B.
B. C.
C. D.
D.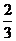
函数极限的求法及灵活应用是本讲的难点,函数的极限大体有以下几种类型:
(1)求函数值法--对于基本初等函数可采用
(2)“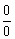 ”型--约去“零因子”(先分解因式),根式先有理化.
”型--约去“零因子”(先分解因式),根式先有理化.
②“ ”型--分子、分母同时除以分母的最高次幂;
”型--分子、分母同时除以分母的最高次幂;
③“∞-∞”型--根式分子有理化,或分解因式.
例4、求下列极限
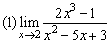
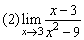
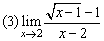

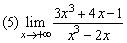
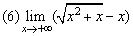
解:
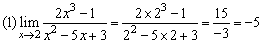 .
.
此法常用于f(x)在x=x0处及其附近有意义,且图象在x=x0处不间断.
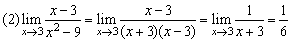 .
.
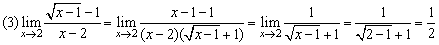 .
.
(2)(3)两例的解法体现了对“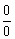 ”型极限计算的一种模式:对分子、分母作适当变形、分解或有理化,约去致使分母为0的公因式,然后再求极限.这里的关键是变形、分解或有理化,应注意对相关知识与技能的运用.
”型极限计算的一种模式:对分子、分母作适当变形、分解或有理化,约去致使分母为0的公因式,然后再求极限.这里的关键是变形、分解或有理化,应注意对相关知识与技能的运用.
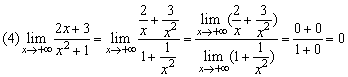 .
.
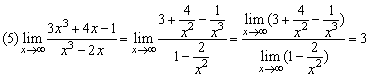 .
.
若a0≠0,b0≠0,m,n为正整数,则
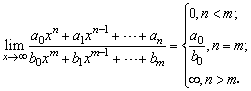
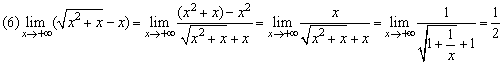 .
.
本题运用分子有理化技能,把“∞-∞型”极限计算转化为“ 型”极限计算,进而利用(4)(5)的模式加以解决,这体现了转化、化归的思想,对这种思想应多领会、多运用.
型”极限计算,进而利用(4)(5)的模式加以解决,这体现了转化、化归的思想,对这种思想应多领会、多运用.
3、常用的函数极限
(1) (2)
(2)
(3) (4)
(4)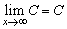
(5)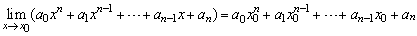
例1、判断下列函数在指定处的极限是否存在:
(1)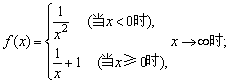
(2)
(3)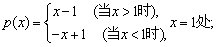
解:
(1)显然,当x→-∞时,f(x)→0;当x→+∞时,f(x)→1.即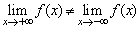 ,故
,故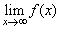 不存在.
不存在.
(2)显然,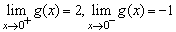 ,故
,故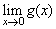 不存在.
不存在.
(3) .
.
例2、求下列各极限:
(1)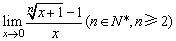 ;
;
(2)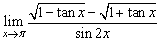
(3)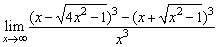 .
.
解:

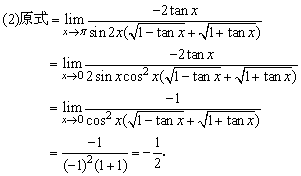

例3、求使下列各式成立的常数a、b的值:
(1) ;
;
(2)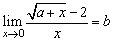 ;
;
(3) .
.
解:
(1)可令x2+ax+b=(x-2)(x+m),则由题意,得 ,于是
,于是 ,∴m=18,再由x2+ax+b=(x-2)(x+18),求得a=16,b=-36.
,∴m=18,再由x2+ax+b=(x-2)(x+18),求得a=16,b=-36.
(2)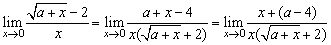 ,
,
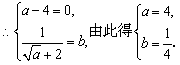
(3)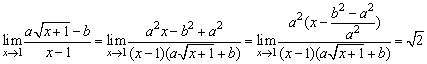
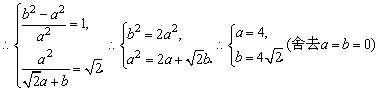
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com