
3. 已知函数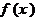 是定义在R上的奇函数,当
是定义在R上的奇函数,当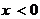 时,
时,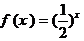 ,则
,则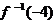 的值是( )
的值是( )
A.2
B.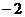 C.3 D.
C.3 D.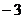
2.若不等式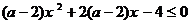 对一切
对一切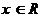 恒成立,则
恒成立,则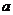 的取值范围是 ( )
的取值范围是 ( )
A.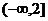 B.
B.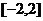 C.
C.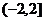 D.
D.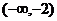
1.已知函数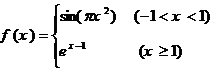 ,若
,若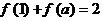 ,则
,则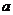 的所有可能值为( )
的所有可能值为( )
A.1
B.1或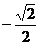 C.
C.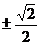 D. 1或
D. 1或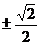
10.(2006北京)已知点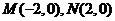 ,动点
,动点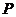 满足条件
满足条件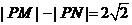 .记动点
.记动点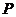 的轨迹为
的轨迹为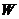 .
.
(Ⅰ)求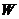 的方程;
的方程;
(Ⅱ)若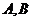 是
是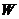 上的不同两点,
上的不同两点,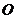 是坐标原点,求
是坐标原点,求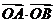 的最小值.
的最小值.
解法一:
(Ⅰ)由|PM|-|PN|=2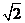 知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长a=
知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长a=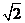 .
.
又半焦距c=2。故虚半轴长b=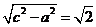 ,
,
所以W的方程为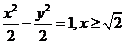
(Ⅱ)设A、B的坐标分别为(x1y1),(x2y2).
当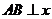 轴时,
轴时,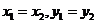 ,从而
,从而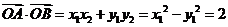 。
。
当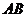 与
与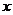 轴不垂直时,设直线
轴不垂直时,设直线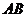 的方程为
的方程为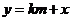 ,与
,与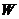 的方程联立,消去
的方程联立,消去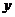 得
得
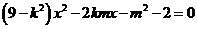 ,
,
故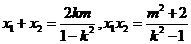
所以
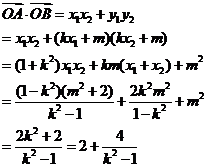
又因为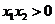 ,所以
,所以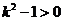 ,从而
,从而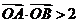 .
.
综上,当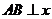 轴时,
轴时,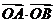 取得最小值2.
取得最小值2.
解法二:
(Ⅰ)同解法一.
(Ⅱ)设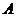 、
、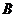 的坐标分别为
的坐标分别为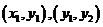 ,则
,则
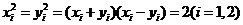
令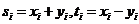 ,
,
则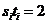 ,且
,且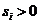 ,
,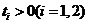 ,所以
,所以
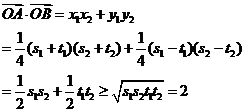
当且仅当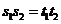 ,即
,即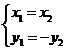 时“=”成立.
时“=”成立.
所以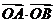 的最小值是2.
的最小值是2.
[探索题](2006安徽)如图,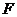 为双曲线
为双曲线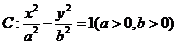 的右焦点,
的右焦点,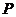 为双曲线
为双曲线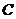 右支上一点,且位于
右支上一点,且位于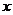 轴上方,
轴上方,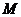 为左准线上一点,
为左准线上一点,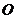 为坐标原点。已知四边形
为坐标原点。已知四边形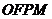 为平行四边形,
为平行四边形,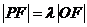 。
。
(Ⅰ)写出双曲线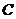 的离心率
的离心率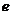 与
与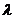 的关系式;
的关系式;
(Ⅱ)当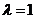 时,经过焦点
时,经过焦点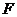 且平行于
且平行于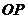 的直线交双曲线于
的直线交双曲线于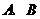 两点,若
两点,若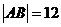 ,求此时的双曲线方程。
,求此时的双曲线方程。
(Ⅰ)解法1:设M′为PM与双曲线右准线的交点,F(c,0),则
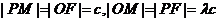
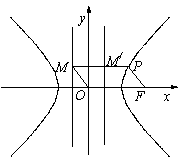

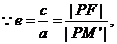
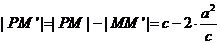
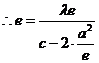
即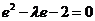
解法2:设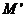 为
为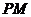 与双曲线右准线的交点,N为左准线与x轴的交点.
与双曲线右准线的交点,N为左准线与x轴的交点.
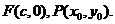 由于
由于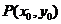 在双曲线右支上,则
在双曲线右支上,则
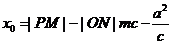 ①
①
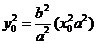 ②
②
由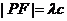 得
得
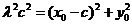 ③
③
将①、②代入③得
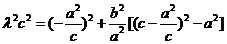
再将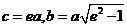 代入上式,得
代入上式,得
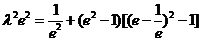
化简,得
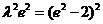 ④
④
由题意,点P位于双曲线右支上,从而
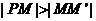
于是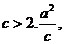 即
即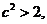 又
又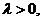 所以由④式得
所以由④式得
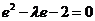
(Ⅱ)解:当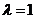 时,由
时,由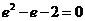 解得
解得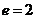
从而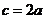 ,
,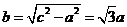
由此得双曲线得方程是
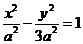
下面确定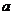 的值
的值
解法1:
设双曲线左准线与x轴的交点为N,P点的坐标为(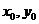 ),则
),则
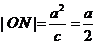 ,
,
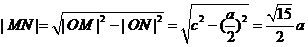
由于P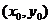 在双曲线的右支上,且位于x轴上方,因而
在双曲线的右支上,且位于x轴上方,因而
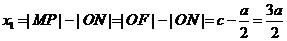 ,
,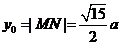
所以直线OP的斜率为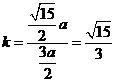
设过焦点F且平行于OP的直线与双曲线的交点为A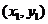 、B
、B ,则
,则
直线AB的斜线为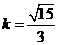 ,直线AB的方程为
,直线AB的方程为
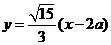
将其代入双曲线方程整理得
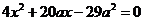
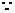
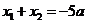 ,
,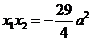
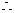
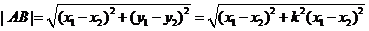
=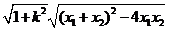
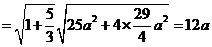
由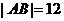 得
得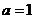 ,于是,所求双曲线得方程为
,于是,所求双曲线得方程为
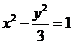
解法2.由条件知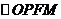 为菱形,其对角线OP与FM互相垂直平分,
为菱形,其对角线OP与FM互相垂直平分,
其交点Q为OP得中点
9.已知抛物线C:y2=4(x-1),椭圆C1的左焦点及左准线与抛物线C的焦点F和准线l分别重合.
(1)设B是椭圆C1短轴的一个端点,线段BF的中点为P,求点P的轨迹C2的方程;
(2)如果直线x+y=m与曲线C2相交于不同两点M、N,求m的取值范围.
(1)解法一:由y2=4(x-1)知抛物线C的焦点F坐标为(2,0).准线l的方程为x=0.设动椭圆C1的短轴的一个端点B的坐标为(x1,y1)(x1>2,y1≠0),点P(x,y),
|
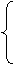
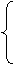
|
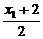 , x1=2x-2,
, x1=2x-2,
y=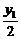 ,
y1=2y.
,
y1=2y.
∴B(2x-2,2y)(x>2,y≠0).
设点B在准线x=0上的射影为点B′,椭圆的中心为点O′,则椭圆离心率e=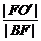 ,由
,由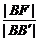 =
=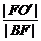 ,得
,得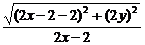 =
=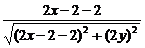 ,
,
整理,化简得y2=x-2(y≠0),这就是点P的轨迹方程.
解法二:抛物线y2=4(x-1)焦点为F(2,0),准线l:x=0.设P(x,y),
∵P为BF中点,
∴B(2x-2,2y)(x>2,y≠0).设椭圆C1的长半轴、短半轴、半焦距分别为a、b、c,
则c=(2x-2)-2=2x-4,b2=(2y)2=4y2,
∵(-c)-(-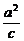 )=2,
)=2,
∴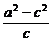 =2,
=2,
即b2=2c.∴4y2=2(2x-4),
即y2=x-2(y≠0),此即C2的轨迹方程.
|
|
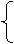 x+y=m,
x+y=m,
y2=x-2
m>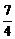 .
.
而当m=2时,直线x+y=2过点(2,0),这时它与曲线C2只有一个交点,
∴所求m的取值范围是(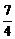 ,2)∪(2,+∞).
,2)∪(2,+∞).
8.(2006上海) 在平面直角坐标系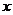 O
O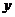 中,直线
中,直线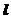 与抛物线
与抛物线 =2
=2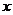 相交于A、B两点
相交于A、B两点
(1)求证:“如果直线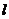 过点T(3,0),那么
过点T(3,0),那么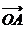
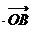 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由
[解](1)设过点T(3,0)的直线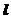 交抛物线y2=2x于点A(x1,y1)、B(x2,y2)
交抛物线y2=2x于点A(x1,y1)、B(x2,y2)
当直线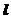 的钭率不存在时,直线
的钭率不存在时,直线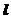 的方程为x=3,此时,直线
的方程为x=3,此时,直线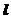 与抛物线相交于点A(3,
与抛物线相交于点A(3,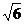 )、B(3,-
)、B(3,-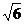 )
) ∴
∴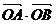 =3;
=3;
当直线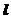 的钭率存在时,设直线
的钭率存在时,设直线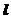 的方程为
的方程为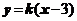 ,其中
,其中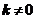 ,
,
由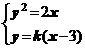 得
得 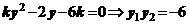
又 ∵
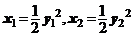 ,
,
∴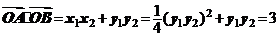 ,
,
综上所述,命题“如果直线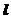 过点T(3,0),那么
过点T(3,0),那么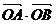 =3”是真命题;
=3”是真命题;
(2)逆命题是:设直线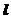 交抛物线y2=2x于A、B两点,如果
交抛物线y2=2x于A、B两点,如果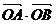 =3,那么该直线过点T(3,0)
=3,那么该直线过点T(3,0) 该命题是假命题
该命题是假命题
例如:取抛物线上的点A(2,2),B(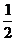 ,1),此时
,1),此时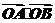 =3,
=3,
直线AB的方程为: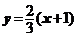 ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;
说明:由抛物线y2=2x上的点A (x1,y1)、B (x2,y2) 满足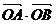 =3,可得y1y2=-6,
=3,可得y1y2=-6,
或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0)
7. 正方形ABCD中,一条边AB在直线y=x+4上,另外两顶点C、D在抛物线y2=x上,求正方形的面积.
解:设CD所在直线的方程为y=x+t,
|
|
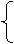 y=x+t,
y=x+t,
y2=x,
x2+(2t-1)x+t2=0,
∴|CD|=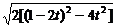
=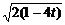 .
.
又直线AB与CD间距离为|AD|=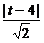 ,
,
∵|AD|=|CD|,
∴t=-2或-6.
从而边长为3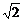 或5
或5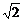 .
.
面积S1=(3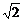 )2=18,S2=(5
)2=18,S2=(5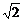 )2=50.
)2=50.
6.设过焦点F(1,0)的直线为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2)
代入抛物线方程消去y得k2x2-2(k2+2)x+k2=0.
∵k2≠0,∴x1+x2=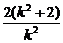 ,
,
|AB|=x1+x2+2=8, x1+x2=6. 可得k2=1.
∴△OAB的重心的横坐标为x=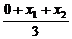 =2.
=2.
.法2:
由|AB|=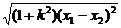 =8, 得k2=1…..
=8, 得k2=1…..
[解答题]
5.设直线l与椭圆交于P1(x1,y1)、P2(x2,y2),
将P1、P2两点坐标代入椭圆方程相减得直线l斜率
k=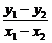 =-
=-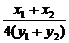 = -
= -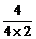 =-
=-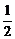 .
.
由点斜式可得l的方程为x+2y-8=0.
答案:x+2y-8=0
4.当x>0时,双曲线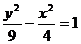 的渐近线为:
的渐近线为: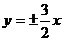 ,而直线y=x+3的斜率为1,1<3/2,因此直线与双曲线的下支有一交点,又y=x+3过椭圆
,而直线y=x+3的斜率为1,1<3/2,因此直线与双曲线的下支有一交点,又y=x+3过椭圆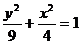 的顶点,k=1>0因此直线与椭圆左半部分有一交点,共计3个交点,选D
的顶点,k=1>0因此直线与椭圆左半部分有一交点,共计3个交点,选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com