
3.正三棱锥 中,
中,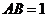 ,侧棱
,侧棱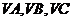 两两互相垂直,则底面中心到侧面的距离为 ( )
两两互相垂直,则底面中心到侧面的距离为 ( )
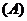
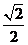
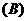
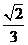
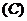
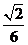
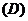

2.正方体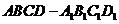 中,
中,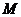 是
是 的中点,
的中点,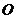 为底面正方形
为底面正方形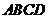 的中心,
的中心,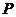 为棱
为棱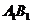 上任意一点,则直线
上任意一点,则直线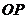 与直线
与直线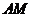 所成的角为 ( )
所成的角为 ( )
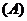

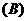
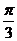
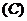
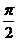
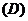 与
与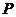 点的位置有关
点的位置有关
1.设正六棱锥的底面边长为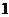 ,侧棱长为
,侧棱长为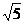 ,那么它的体积为 ( )
,那么它的体积为 ( )
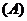
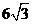
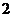
例1.设向量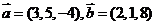 ,计算
,计算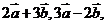
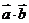 及
及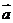 与
与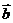 的夹角,并确定当
的夹角,并确定当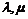 满足什么关系时,使
满足什么关系时,使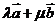 与
与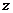 轴垂直.
轴垂直.
例2.棱长为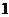 的正方体
的正方体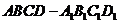 中,
中,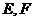 分别为
分别为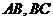 的中点,试在棱
的中点,试在棱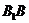 上找一点
上找一点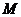 ,使得
,使得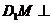 平面
平面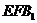 。
。
例3.已知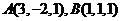 ,
,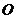 为坐标原点,
为坐标原点,
(1)写出一个非零向量 ,使得
,使得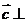 平面
平面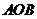 ;
;
(2)求线段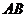 中点
中点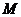 及
及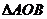 的重心
的重心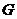 的坐标;
的坐标;
(3)求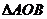 的面积。
的面积。
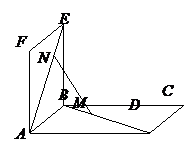 例4.如图,两个边长为1的正方形
例4.如图,两个边长为1的正方形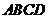 与
与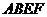 相交于
相交于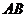 ,
, 分别是
分别是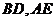 上的点,且
上的点,且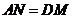 ,
,
(1)求证: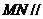 平面
平面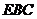 ;
;
(2)求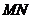 长度的最小值。
长度的最小值。
5.已知向量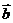 与向量
与向量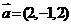 共线,且满足
共线,且满足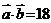 ,
,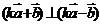 ,
,
则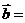 ,
, 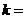 。
。
4.设向量 ,若
,若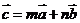 ,
,
则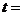 ,
,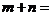 。
。
3.已知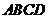 为平行四边形,且
为平行四边形,且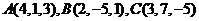 ,则点
,则点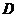 的坐标为_____.
的坐标为_____.
2.已知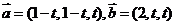 ,则
,则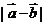 的最小值是
( )
的最小值是
( )
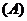

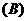

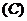
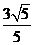
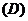
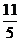
1. 已知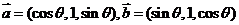 ,则向量
,则向量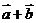 与
与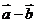 的夹角是 ( )
的夹角是 ( )
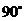
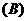

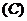
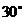
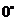
(1)空间向量的坐标:空间直角坐标系的x轴是横轴(对应为横坐标),y轴是纵轴(对应为纵轴),z轴是竖轴(对应为竖坐标).
①令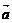 =(a1,a2,a3),
=(a1,a2,a3),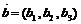 ,则
,则
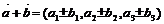
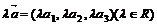

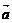 ∥
∥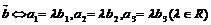
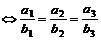
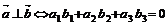
 (用到常用的向量模与向量之间的转化:
(用到常用的向量模与向量之间的转化: )
)
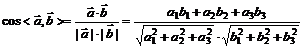
②空间两点的距离公式: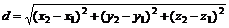 .
.
(2)法向量:若向量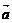 所在直线垂直于平面
所在直线垂直于平面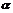 ,则称这个向量垂直于平面
,则称这个向量垂直于平面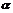 ,记作
,记作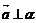 ,如果
,如果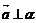 那么向量
那么向量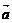 叫做平面
叫做平面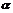 的法向量.
的法向量.
(3)用向量的常用方法:
①利用法向量求点到面的距离定理:如图,设n是平面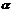 的法向量,AB是平面
的法向量,AB是平面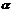 的一条射线,其中
的一条射线,其中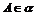 ,则点B到平面
,则点B到平面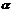 的距离为
的距离为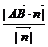 .
.
②利用法向量求二面角的平面角定理:设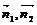 分别是二面角
分别是二面角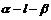 中平面
中平面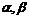 的法向量,则
的法向量,则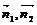 所成的角就是所求二面角的平面角或其补角大小(
所成的角就是所求二面角的平面角或其补角大小(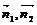 方向相同,则为补角,
方向相同,则为补角,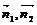 反方,则为其夹角).
反方,则为其夹角).
③证直线和平面平行定理:已知直线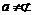 平面
平面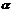 ,
,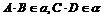 ,且CDE三点不共线,则a∥
,且CDE三点不共线,则a∥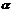 的充要条件是存在有序实数对
的充要条件是存在有序实数对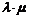 使
使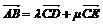 .(常设
.(常设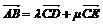 求解
求解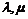 若
若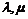 存在即证毕,若
存在即证毕,若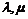 不存在,则直线AB与平面相交).
不存在,则直线AB与平面相交).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com