
7.(2008·全国Ⅱ文)设向量a=(1,2),b=(2,3),若向量 a+b与向量c=(-4,-7)共线,则
a+b与向量c=(-4,-7)共线,则 = .
= .
答案 2
6.设0≤ <2
<2 ,已知两个向量
,已知两个向量 =(cos
=(cos ,sin
,sin ),
), =(2+sin
=(2+sin ,2-cos
,2-cos ),则向量
),则向量 长度的最大值是
.
长度的最大值是
.
答案 3
5.(2008·辽宁文)已知四边形ABCD的顶点A(0,2)、B(-1,-2)、C(3,1),且 =2
=2 ,则顶点D的坐标为 .
,则顶点D的坐标为 .
答案 
4.(2007·北京文)已知向量a=(2,4),b=(1,1),若向量b⊥(a+ b),则实数
b),则实数 的值是 .
的值是 .
答案 -3
3.已知向量 =(3,-2),
=(3,-2), =(-5,-1),则
=(-5,-1),则
 =
.
=
.
答案 
2.设a、b是不共线的两个非零向量,已知 =2a+pb,
=2a+pb, =a+b,
=a+b, =a-2b.若A、B、D三点共线,则
=a-2b.若A、B、D三点共线,则
p的值为 .
答案 -1
1.已知向量a=(2,3),b=(-1,2),若ma+nb与a-2b共线,则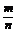 = .
= .
答案 -
12.(2008·湛江模拟)如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,
 E是棱CC1上的点,且BE⊥B1C.
E是棱CC1上的点,且BE⊥B1C.
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE所成角的正弦值.
(1)解 如图所示,以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D-xyz.
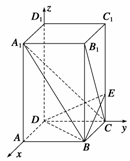 ∴D(0,0,0),A(2,0,0),B(2,2,0),
∴D(0,0,0),A(2,0,0),B(2,2,0),
C(0,2,0),A1(2,0,4),
B1(2,2,4),C1(0,2,4),D1(0,0,4).
设E点坐标为(0,2,t),则 =(-2,0,t),
=(-2,0,t), =(-2,0,-4).
=(-2,0,-4).
∵BE⊥B1C,
∴ ·
· =4+0-4t=0.∴t=1,故CE=1.
=4+0-4t=0.∴t=1,故CE=1.
(2)证明 由(1)得,E(0,2,1), =(-2,0,1),
=(-2,0,1),
又 =(-2,2,-4),
=(-2,2,-4), =(2,2,0),
=(2,2,0),
∴ ·
· =4+0-4=0,
=4+0-4=0,
且 ·
· =-4+4+0=0.
=-4+4+0=0.
∴ ⊥
⊥ 且
且 ⊥
⊥ ,即A1C⊥DB,A1C⊥BE,
,即A1C⊥DB,A1C⊥BE,
又∵DB∩BE=B,∴A1C⊥平面BDE.
即A1C⊥平面BED.
(3)解 由(2)知 =(-2,2,-4)是平面BDE的一个法向量.又
=(-2,2,-4)是平面BDE的一个法向量.又 =(0,2,-4),
=(0,2,-4),
∴cos〈 ,
, 〉=
〉= =
= .
.
∴A1B与平面BDE所成角的正弦值为 .
.
11.如图所示,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,
OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小;
(2)当k取何值时,二面角O-PC-B的大小为 ?
?
解 ∵OP⊥平面ABC,又OA=OC,AB=BC,
 从而OA⊥OB,OB⊥OP,OA⊥OP,
从而OA⊥OB,OB⊥OP,OA⊥OP,
以O为原点,建立如图所示空间直角坐标系O-xyz.
(1)设AB=a,则PA=a,PO= a,
a,
A( a,0,0),B(0,
a,0,0),B(0, a,0),
a,0),
C(- a,0,0),P(0,0,
a,0,0),P(0,0, a),
a),
则D(- a,0,
a,0, a).
a).
∵ =(
=( a,0,-
a,0,- a ),
a ), =(-
=(- a,-
a,- a,
a, a),
a),
∴cos〈 ,
, 〉=
〉= =
= =-
=- ,
,
则异面直线PA与BD所成角的余弦值的大小为 .
.
(2)设AB=a,OP=h,∵OB⊥平面POC,
∴ =(0,
=(0, a,0)为平面POC的一个法向量.
a,0)为平面POC的一个法向量.
不妨设平面PBC的一个法向量为n=(x,y,z),
∵A( a,0,0),B(0,
a,0,0),B(0, a,0),C(-
a,0),C(- a,0,0),P(0,0,h),
a,0,0),P(0,0,h),
∴ =(-
=(- a,-
a,-  a,0),
a,0), =(-
=(-  a,0,-h),
a,0,-h),
由


不妨令x=1,则y=-1,z=- ,
,
即n=(1,-1,-  ),则cos
),则cos =
=
= =
=
 2+
2+ =4
=4 h=
h= a,
a,
∴PA= =
= =
= a,
a,
而AB=kPA,∴k= .
.
故当k= 时,二面角O-PC-B的大小为
时,二面角O-PC-B的大小为 .
.
10. 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=2
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=2 a,BC=DE=a,∠EAB=∠ABC=
a,BC=DE=a,∠EAB=∠ABC=
∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E的余弦值.
(1)证明 以A点为坐标原点,以AB、AE、AP所在直线分别为x、y、z轴,建立空间直角坐标系A-xyz,则由已知得
A(0,0,0),P(0,0,2a),
 B(2a,0,0),C(2a,a,0),
B(2a,0,0),C(2a,a,0),
D(a,2a,0),E(0,2a,0).
∴ =(0,0,2a),
=(0,0,2a), =(2a,0,0),
=(2a,0,0), =(0,2a,0),
=(0,2a,0),
∴ ·
· =0·2a+0·0+2a·0=0,
=0·2a+0·0+2a·0=0,
∴ ⊥
⊥ .同理
.同理 ⊥
⊥ .
.
又∵AB∩AE=A,∴PA⊥平面ABCDE.
(2)解 设平面PAD的法向量为m=(1,y,z),
则m· =0,得a+2ay=0,∴y=-
=0,得a+2ay=0,∴y=- .
.
又m· =0,得2az=0,∴z=0.
=0,得2az=0,∴z=0.
∴m=(1,- ,0).
,0).
再设平面PDE的法向量为n=(x,1,z),
而 =(a,0,0),
=(a,0,0), =(a,2a,-2a),
=(a,2a,-2a),
则n· =0,得ax=0,∴x=0.
=0,得ax=0,∴x=0.
又n· =0,得ax+2a-2az=0,∴z=1.
=0,得ax+2a-2az=0,∴z=1.
∴n=(0,1,1).
令二面角A-PD-E的平面角为 ,
,
则cos =-
=- =
= =
= ,
,
故二面角A-PD-E的余弦值是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com