
中央集权制度是中国古代基本的政治制度。据此回答1-3题。
1.秦朝中央集权制度的主要特点有( )
①皇权至上 ②三公九卿之间互相配合,互相牵制 ③刺史代表中央监察地方 ④郡守、县令均由朝廷任命
A.①②④ B.②③④ C.①②③ D.①③④
2.(07年高考全国文综卷Ⅱ)隋唐实行三省六部制。唐初三省的职能是( )
A.尚书省和中书省决策,门下省执行 B.中书省决策,门下省和尚书省执行
C.门下省决策,中书省和尚书省执行 D.中书省和门下省决策,尚书省执行
3.中央集权与地方分权的斗争是中国古代政治史上的重要内容。下列属于加强中央集权的措施有( )
①秦朝皇帝直接任命郡县长官②隋唐确立和完善三省六部制③北宋任用文臣做地方长官④明朝废除丞相
A.①⑧ B.②③④ C.①③④ D.①②③④
数学充满着辩证法,一般性往往寓于特殊性之中。解题时,将一般问题特殊化和将特殊问题一般化是常用的两种策略。对一些较为抽象或一般规律又无显露的数学问题,尤其是答案相对唯一的选择题,可以采用抽象问题具体化,一般问题特殊化的方法来验证,而无需作费时费力的严格推证,从而避免“小题大做”,以降低难度,尽快确定正确答案。
 例6、(2001年全国高考)一间民房的屋顶有如下图三种不同的盖法:
例6、(2001年全国高考)一间民房的屋顶有如下图三种不同的盖法:
①单向倾斜;②双向倾斜;③四向倾斜。记三种盖法屋顶面积分别为P1、P2、P3。若屋顶斜面与水平面所成的角都是α,则( ) (A)P3=P2>P1 (B)P3>P2=P1 (C)P3>P2>P1 (D)P3=P2=P1
分析:由射影面积公式(  )可知:
)可知: 与斜面和水平面所成角
与斜面和水平面所成角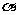 有关,而与斜面内图形形状及图形放置无关。所以可以抓住“所成角都是
有关,而与斜面内图形形状及图形放置无关。所以可以抓住“所成角都是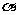 ”及“射影面积(民房面积)不变”,取特值
”及“射影面积(民房面积)不变”,取特值 ,就将三种不同的房盖均变成平房盖,而同一间民房的面积全部相同,从而得解。
,就将三种不同的房盖均变成平房盖,而同一间民房的面积全部相同,从而得解。
解:令 ,即可知选D。
,即可知选D。
当然,除了上述常用方法外,数学解题中还存在其它的转化方法,如:在求空间距离问题时,可利用等积法(点线距离常用等面积法,点面距离常用等体积法)将它转化为解三角形的问题;在求空间角(异面直线所成的角或二面角的平面角)时,可通过平移变换、作辅助线等方法转化为同一个平面或三角形中;而求函数的值域(或最值),有时也可以根据反函数的性质,通过求该函数的反函数的定义域来得到。……由于本文篇幅有限,这里就不一一举例。
总而言之,化归与转化的思想具有灵活性和多样性的特点,没有统一的模式可遵循,需要依据问题本身提供的信息,利用动态思维,去寻找有利于问题解决的变换途径和方法,所以学习和熟悉化归与转化的思想,有意识地运用数学变换的方法,去灵活地解决有关的数学问题,将有利于提高解决数学问题的应变能力和技能、技巧。
对结构较为复杂,量与量之间的关系不甚明了的命题,通过适当的引入新变量(换元),往往可以简化原有结构,使其转化为便于研究的形式。常用的换元法有代数代换、三角代换、整体代换等。在应用换元法时要特别注意新变量的取值范围,即代换的等价性。
例5、(2004年高考广西理科)解方程:
分析:若令 ,(
,( ),则原方程可转化为求含绝对值的二次方程的解。
),则原方程可转化为求含绝对值的二次方程的解。
解:令 ,(
,( ),原方程可化为:
),原方程可化为:
①当 (即
(即 )时,方程可化为:
)时,方程可化为: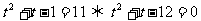
解之得: ,或
,或 (不舍题意,舍去)
(不舍题意,舍去)

②当 (即
(即 )时,方程可化为:
)时,方程可化为:
解之得: 或
或 (均不舍题意,舍去)
(均不舍题意,舍去)
所以,原方程的解为 
函数与方程的思想是求数量关系的主要思想方法。一个数学问题,如能建立描述其数量特征的函数表达式,或列出表示其数量关系的方程式(组)(包括不等式(组)),则一般可使问题得到解答。
例4、已知平行四边形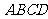 中,点
中,点 的坐标分别为(
的坐标分别为( ,点
,点 在椭圆
在椭圆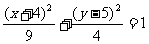 上移动,求点
上移动,求点 的轨迹方程。
的轨迹方程。
分析:因为平行四边形的对边平行且相等,所以可以将本题转化为相等向量的性质来求解。
解:设 的坐标分别为
的坐标分别为
则
 在平行四边形
在平行四边形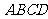 中,
中,


 点
点 在椭圆上,
在椭圆上,
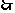 把
把 点坐标
点坐标 代入椭圆方程中,
代入椭圆方程中,
即得点 的轨迹方程:
的轨迹方程: 
数形结合的思想就是把问题的数量关系和空间形式结合起来加以考察的思想,其实质就是把抽象的数量关系和直观的图形结合起来,从而降低原命题的难度,使问题容易得到解决。
例3、如果实数 满足
满足 ,那么
,那么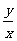 的最大值是( )
的最大值是( )
A. B.
B. C.
C. D.
D.
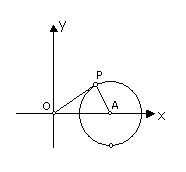 分析:由于方程
分析:由于方程 表示的曲线以
表示的曲线以 为圆心,以
为圆心,以 为半径的圆(如右图所示),满足方程的
为半径的圆(如右图所示),满足方程的 是圆上的点
是圆上的点 ;而
;而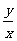 是坐标原点
是坐标原点 与圆上各点连线的斜率,所以题目可转化为求原点
与圆上各点连线的斜率,所以题目可转化为求原点 与圆上各点连线的斜率的最大值。结合图像,易知直线
与圆上各点连线的斜率的最大值。结合图像,易知直线 与圆
与圆 相切的时候,直线
相切的时候,直线 的斜率
的斜率 就是所求斜率的最大值。
就是所求斜率的最大值。
解:


即所求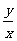 的最大值是
的最大值是 ,故选D。
,故选D。
如果一个命题从正面解决不好入手或比较麻烦,可以从命题的反面入手来解决。如:证明命题的唯一性、无理性,或所给的命题以否定形式出现(如:不存在、不相交等),并伴有“至少”“不都”“都不”“没有”等指示性词语时,均可考虑用反证法的思想来实现转化。反证法是数学解题中逆向思维的直接体现。
例2、已知下列三个方程: ,
, ,
, 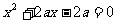 中,至少有一个方程有实根,求实数
中,至少有一个方程有实根,求实数 的取值范围。
的取值范围。
分析:此题若采用正面讨论,则必须分成“有且只有一个方程有实根”,“有两个方程有实根”和“三个方程全部有实根”三种不同情况来讨论,求解过程将会非常复杂。所以,应采用补集和反证法的思想来求。
解:若方程没有一个有实根,则有
解之得:
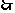 满足三个方程至少有一个方程有实根的
满足三个方程至少有一个方程有实根的 的解集是
的解集是 。
。
在数学中,存在许许多多具有等价性的问题,“恒等变形”是解题的最基本的方法,如解方程和不等式的过程本身就是一个等价转化的过程。
例1、(2003年全国高考)已知 。设
。设 函数
函数 在
在 上单调递减。
上单调递减。 不等式
不等式 的解集为
的解集为 。如果
。如果 和
和 有且仅有一个正确,求
有且仅有一个正确,求 的取值范围。
的取值范围。
分析:“ 和
和 有且仅有一个正确”等价于“
有且仅有一个正确”等价于“ 正确且
正确且 不正确”或“
不正确”或“ 不正确且
不正确且 正确”,所以应先求出
正确”,所以应先求出 和
和 分别正确时的解集,再用集合间的关系来运算。
分别正确时的解集,再用集合间的关系来运算。
解: 函数
函数 在
在 上单调递减
上单调递减
 不等式
不等式 的解集为
的解集为
 函数
函数 在
在 上恒大于1。
上恒大于1。


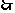 函数
函数 在
在 上的最小值为
上的最小值为 。
。
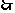 不等式
不等式 的解集为
的解集为
 。
。
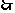 如果
如果 正确且
正确且 不正确,则
不正确,则
如果 不正确且
不正确且 正确,则
正确,则
所以 的取值范围为
的取值范围为 。
。
8.(★★★★★)It’s a fine day. Let’s go fishing,________?
A.won’t we B.will we
C.don’t we D.shall we (NMET1990)
7.(★★★★★)She hardly ever speaks to you in English, ________?
A.does she B.doesn’t she
’t she
6.(★★★★★)Don’t smoke in the meeting room,________?
A.do you B.will you
you D.could you (NMET1991)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com