
20.(本题满分14分)
已知f(x)= x-ln(-x),x∈[-e,0),
x-ln(-x),x∈[-e,0), ,其中e=2.71828…是自然对数的底数,
,其中e=2.71828…是自然对数的底数, ∈R.
∈R.
(1)若 =-1,求f(x)的极值;
=-1,求f(x)的极值;
(2)求证:在(1)的条件下, ;
;
(3)是否存在实数 ,使f(x)的最小值是3,如果存在,求出
,使f(x)的最小值是3,如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
中山市高二级2008-2009学年度第二学期期末统一考试
19.(本题满分14分)
如右图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为 km.
km.
(1)按下列要求写出函数关系式:
①设∠BAO= (rad),将
(rad),将 表示成
表示成 的函数;②设OP
的函数;②设OP (km)
,将
(km)
,将 表示成
表示成 的函数.
的函数.
 (2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.
18.(本题满分13分)
根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01.该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元.
方案2:建保护墙,建设费为2000元.但围墙只能防小洪水.
方案3:不采取措施,希望不发生洪水.
试比较哪一种方案好?
17.(本题满分13分)
袋中有20个大小相同的球,其中记上0号的有10个,记上 号的有
号的有 个(
个( ).现从袋中任意取一球,
).现从袋中任意取一球, 表示所取球的标号.
表示所取球的标号.
(1)求 的分布列、期望和方差;
的分布列、期望和方差;
(2)若 ,
, =1,
=1, =11,试求
=11,试求 、
、 的值.
的值.
16.(本题满分13分)
 已知
已知 是
是
 内任意一点,连结
内任意一点,连结 ,
, ,
, 并延长交对边于
并延长交对边于 ,
, ,
, ,则
,则 . 这是平面几何中的一个命题,其证明方法常采用“面积法”:
. 这是平面几何中的一个命题,其证明方法常采用“面积法”: .运用类比猜想,对于空间四面体存在什么类似的命题?并用“体积法”证明.
.运用类比猜想,对于空间四面体存在什么类似的命题?并用“体积法”证明.
15.(本题满分13分)
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
|
转速x(转/秒) |
16 |
14 |
12 |
8 |
|
每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(1)利用散点图或相关系数r的大小判断变量y对x是否线性相关?为什么?
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据: ,
,
 ,
, ,
, =291).
=291).
14.从以下三个小题中选做一题(请回答且只能回答其中一个,回答两个或两个以上的,按得分最低的记分).
(1)(不等式选讲选做题)已知 ,若关于
,若关于 的方程
的方程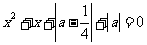 有实根,则
有实根,则 的取值范围是 .
的取值范围是 .
(2)(坐标系与参数方程选做题)已知曲线 、
、 的极坐标方程分别为
的极坐标方程分别为 ,
,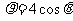
 ,则曲线
,则曲线 、
、 交点的极坐标为 .
交点的极坐标为 .
(3)(几何证明选讲选做题)已知PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R= .
13.若函数f(x)=x3-3a2x+1的图象与直线y=3只有一个公共点,则实数a的取值范围为__________.
12.从 概括出第
概括出第 个式子为___________.
个式子为___________.
11. 某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有_________种.(用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com