2、集合A={3－2x，1，3}，B={1，x²}，并且A∪B=A，那么满足条件的实数x个数有………(　　 )

(A)1　　　 　　　　　(B) 2　　　　 　　　　　(C)3　　　　　　　 (D) 4

1、全集I={x|x≤4，x∈N*}，A={1，2，3}，A∩={2，3}，那么B=…………(　　 )

(A){2，3}　　　　　 (B) {2，3}或者{2，3，4} (C){1，4}　　　　　 (D) {1，4}或者{1}

学会了解

了解犹如那春日里的阳光，让你我彼此之间的心连在了一起，更加的温暖；了解犹如那沙漠里的一丝甘泉，让你我彼此之间的心灵得到了滋润，更加的甘甜；了解犹如那宽阔大海中的一艘小船，让你我彼此之间的距离拉近了，更加的友好……

无论是寒冷的冬天，还是炎热的夏天，我们都需要彼此之间的了解。因此，我们首先要学会了解。只有自己学会了了解，才能彼此了解。

了解可以使我们辩清事实，做出取舍。

了解了事实，辩清了事实，我们才能选取好的，对我们有益的东西，屏弃无用的东西。

陶渊明了解了官场的腐败，不愿为五斗米折腰，毅然放弃了做官，走上了其向往的田园生活，给我们留下了优美的田园小诗；李白了解权贵的腐败，高呼“安能翠眉折腰事权贵，使我不得开心颜！”走上了难于上青天的蜀道，造就了他的浪漫主义诗篇……就是因为陶渊明和李白对官场、权贵的了解，使得他们辩清了事实，做出了正确的取舍，才给我们留下了巨大的精神财富！

因此，我们要学会了解。

了解可以使我们事半功倍，成就更大的辉煌。

了解可以使我们做事有计划、有条理，能让我们抓住关键，达到事半功倍的效果。

“庖丁解牛”的故事，相信大家都知道。就是因为庖丁对牛内部结构的了解，使得他解起牛来有条理、有层次，最终事半功倍；钟南山就是由于他对生物知识的了解，使得他很快地发现SARS病毒的冠状结构，为获得SARS抗战的胜利奠定了基础，挽救了无数人的生命……

可见，了解是那么的重要。因此，我们要学会了解。

了解需要我们用心的去观察，去领悟。

了解就是那淳香的茶，需要我们用心去品尝；了解就是那博大精深的自然原理，需要我们用心去领悟……

无论我们面对的是何种事物，我们都应该摆出真诚的心，用心的去倾听；无论我们面对的是何种事物，我们都要献上我们真诚的心，用心的去倾听…… 　　 春夏秋冬，日夜更替，我们无时无刻都需要了解，让我们学会了解，让我们的世界放射出更加灿烂、和谐的光芒！

面对问题，应使用正确的方法

在生活中，人总是会遇到各种各类的问题，如小学生遇到不认识的字，公车司机遇到交通阻塞，大公司遇到资金周转不灵等，这不都是使面对者犯愁的问题吗？但如何处理呢？搁置不理吗？不，面对问题时，我们应该寻找正确的方法，使之解决。

正确的方法，能使问题得到解决。遇到问题时，人是否乱打乱撞地就得解决它呢？或许，碰巧也能解决一两个，但这一两个问题的解决，也是因为你幸运能误打误撞找到了它们正确的解决方法，才得以迎刃而解。所以，想要解决问题，必须要有一个正确解决问题的方法。秦始皇用暴力统一天下，结束了古代四分五裂的局面，倘若秦始皇当时并不是用暴力，而是像一些文人那样，通过写诗、写文章或是传教等来统一天下，他能成功吗？不能，在当时，政治动荡、时局混乱的情况下，除了使用武力外，其他的方法是难以统一天下的。因此，正确的方法是能使问题解决的。

怎样寻找解决问题的正确方法呢？是否任何方法都能解决所有问题？不，一个问题是有解决它的方法的，但并不是所有方法都可以，想要找到问题的解决方法，就必须从实际出发。我国“人”字形铁路的建成，是件震惊中外的史实，当时，我国要修建一条从北京到张家界的铁路，本来是由英国人来建的，但因为俄国人说那是他们管理的地方，应该是由他们来建不能把修建权给了英国。经过争论之下，最终修建权落到了中国人自己的头上。因为他们要看中国人出洋相。为什么这么说呢？因为修建铁路的地方，地形十分崎岖。对于这样地形要修建铁路是十分困难的。当时担任“总工程师”的詹天佑为了让这个人蒙羞，他带着两名学员，带着简陋的工具，亲自考察地形，从实际出发，最终被他建造出“人”字形的铁路，震惊中外。因此，找到正确的方法，必须从问题的缺口入手。 　　 在生活中，面对什么的问题都不要慌，因为它总会有解决的方法，只要找到，问题就能解决！

开启困难的锁

困难犹如一把坚实的锁，只有用在逆境中磨砺出的精神--钥匙，才能打开这把坚实的锁，去开启成功之门。让我们用钥匙去开启困难之锁。

用坚持不懈、永不言弃的精神，才能开启学习上困难的锁，取得成功。学习上遇到困难是难免的，学习贵在坚持，不能被一点的困难而吓倒。我国著名的女学者张海迪，她虽高位截瘫，病后连口音都说不正，但他并没有因此而放弃自己的梦想，而是每天用自己坚强的意志对着镜子读英语，日复一日，年复一年，从来没有停下来，终于让她在学习上取得了巨大的成功，翻译了许多外语书籍，让自己的名字家喻户晓。如果说张海迪患病后就消沉，遇到困难就退缩，那么她只能是个真正的残疾人了。可见，在学习上要取得成功，坚持不懈，永不言弃的精神是十分重要的。

用不畏困难，勇往直前的意志，才能开启事业上困难的锁，取得辉煌。昔日文王拘而演《周易》，仲尼厄而作《春秋》，屈原放逐乃赋《离骚》……当年伟大的马克思被很多人排挤，而他不畏别人的指责，一直坚持真理，终于让《共产党宣言》诞生了，为人类社会的进步，历史的发展作出了巨大贡献。正是因为他们在困难面前不屈不挠，用自己的意志战胜了困难，从困难的磨砺中让自己拥有了一把钥匙，才能打开困难之锁，打开成功之门。可见，拥有不屈不挠，勇往直前的意志，是开启困难之锁必不可少的条件。

用积极乐观，从容豁达的心态，才能开启人生路上困难的锁，获得成就。当我们面对困难时，拥有乐观豁达的心态，才能轻松自信地去解决问题。宋代词人苏轼，他在遭受仕途的不顺后，并没有让自己整天愁眉苦脸，意志消沉，而是“竹杖芒鞋轻胜马”“谁怕”人生路上的风雨？他以豁达的心态“一蓑烟雨任平生”。是的，在人生的逆境中，有乐观豁达的心态，就能把问题缩小，困难就会迎刃而解了。可见，乐观豁达的心态，是助我们开启困难之锁的润滑剂。 　　 让我们用那把坚持不懈，不畏困难，积极乐观的钥匙去开启那把困难之锁吧，去打开成功之门吧。

学会了解，理解的重要性，谈成功，面对困难的方法，解决问题的关键，打开成功大门的钥匙……

哪些观点是正确的，哪些观点是错误的？

怎么知道对错呢？我们可以用正确的审题方法来试一试，那正确的审题方法有哪些呢？

1、抓住关键词句法。2、因果推断法。3、明辩关系法。4、对应“人生”法(适合比喻、象征型题目)(具体内容参看《作文备考教程(五)》)

7．如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC,AC⊥BD,AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2,PO=,PB⊥PD．

(1)求异面直线PD与BC所成角的余弦值；

(2)求二面角P－AB－C的大小；

(3)设点M在棱PC上，且为何值时，PC⊥平面BMD．

解： 平面

,又，，

由平面几何知识得：

以为原点，分别为轴建立如图所示的空间直角坐标系，则各点坐标为，，，，，

(1)，　 ，。

。

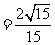故直线与所成的角的余弦值为

(2)设平面的一个法向量为，

由于，，

由　 得　 取，

又已知平面ABCD的一个法向量，

,

又二面角为锐角，所求二面角的大小为

(3)设，由于三点共线，，

平面，

由(1)(2)知：，。

，故时，平面。

考查运用空间向量的有关知识求空间的角和距离．要求掌握利用空间向量求空间的角和距离的一般方法．

利用空间向量求异面直线所成角时,必须注意异面直线所成角的范围是(0，,向量的夹角的范围是[0，,故向量的夹角与异面直线的夹角可能相等，也可能互补。

求直线与平面所成角：先求出平面的法向量，再求此直线所在向量与法向量所成角(锐角)，它的余角为线面角；

求两个平面所成角:二面角的大小转化为求面的法向量m、n的夹角<m，n>或其补角。

空间的距离有：可以利用|a|=aa，进行计算。

6．如图，已知正三棱柱ABC-A₁B₁C₁的侧棱长和底面边长均为1，M是底面BC边上的中点，N是侧棱CC₁上的点，且CN＝2C₁N．

(1)求二面角B₁－AM－N的平面角的余弦值；

(2)求点B₁到平面AMN的距离。

解：(1)建立如图所示的空间直角坐标系，则(0，0，1)，M(0，，0),C(0,1,0), N (0,1,) , A ()，

所以，，,。

因为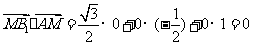

所以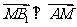,同法可得。

故﹤﹥为二面角-AM-N的平面角

∴﹤﹥＝

故所求二面角-AM-N的平面角的余弦值为。

(2)设n=(x,y,z)为平面AMN的一个法向量，则

由得．故可取

设与n的夹角为a，则。

所以到平面AMN的距离为。