
3、(2009年贵阳市)如图20甲所示,当开关S接a时,移动滑动变阻器的滑片P,根据测出的电流、电压值,画出了定值电阻R0的U-I图像;当开关S接b时,同样根据测出的电流、电压值,画出了灯泡L的U-I图像,如图20乙所示。
(1)求定值电阻R0的阻值;
(2)将R0与灯L串联接在6V的电源两端时,求灯丝的实际电阻值;
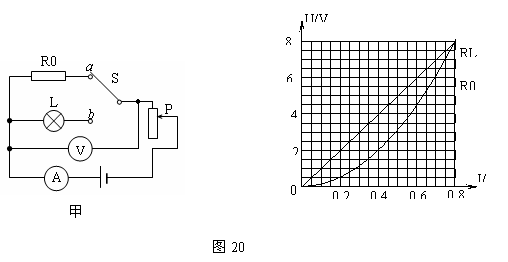 (3)将R0与灯L并联接入电路并调节电源电压,当 R0消耗的电功率为4.9W时,灯L恰好正常发光,求灯L的额定电功率。
(3)将R0与灯L并联接入电路并调节电源电压,当 R0消耗的电功率为4.9W时,灯L恰好正常发光,求灯L的额定电功率。
答案:解:⑴由图像可知:当U0 =2V 时, I0=0.2A(利用其它数据也可)
∴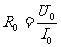 =
=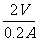 =10Ω
(2分)
=10Ω
(2分)
(2)分析图像可知:此时UL=2V IL =0.4A
∴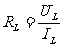 =
=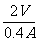 =5Ω
(2分)
=5Ω
(2分)
(3)∵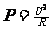 ∴U0′=
∴U0′=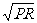 =
=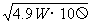 =7V
=7V
∵R0与RL并联 且灯正常发光 ∴UL额=U0′=7V
由图像可知此时:IL额=0.75A
故:PL额= UL额IL额=7V×0.75A=5.25W (2分)
1.(2009年安顺市)如图7 所示,电源电压恒定。小灯泡L标有“3V 0.6W”字样,R为定值电阻,闭合S,断开S1,小灯泡正常发光;若再闭合S1,发现电流表示数变化0.3A ,则R的阻值为___①__W,此时灯泡L和电阻R消耗的功率之比是__②___ 。答案:10,2:3。
2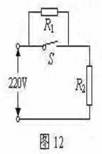 .(2009年安顺市)(10分)某中学为解决同学们的饮水问题,新购置了一批台式饮水机,其铭牌如下表所示.图12 是饮水机的电路图,S是用感温材料制造的温控开关,R1是电阻,R2是供加热的电阻丝.分析电路图可知,当S接通时,饮水机处于加热状态,当S断开时处于保温状态。
.(2009年安顺市)(10分)某中学为解决同学们的饮水问题,新购置了一批台式饮水机,其铭牌如下表所示.图12 是饮水机的电路图,S是用感温材料制造的温控开关,R1是电阻,R2是供加热的电阻丝.分析电路图可知,当S接通时,饮水机处于加热状态,当S断开时处于保温状态。
|
额定频率 |
50Hz |
环境温度 |
10℃-38℃ |
|
加热功率 |
550W |
环境湿度 |
≤90% |
|
额定电压 |
220V |
制热水能力 |
≥90℃ 5L/h |
(1)在加热状态下,饮水机正常工作时电路中的电流是多大?
(2)正常工作时该饮水机将热水罐中0.6kg,l8℃的水加热到93℃,用时6min。用这些数据及题目中的信息,计算热水罐中的水吸收的热量和该饮水机加热状态时的效率。[C水=4.2×103J /(kg·℃)](4分)
(3)如果要使饮水机在保温状态时的功率是加热状态时的一半,则R1与R2的比值应是多少?( 4分)
答案:解:(1)由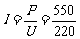 ………………………………………………(1分)
………………………………………………(1分)
= 2.5(A) ………………………………………………(1分)
(2)Q吸 = c水m(t-t0)= 4.2×103×0.6×(93-18) ……………………(1分)
= 1.89×105(J) ………………………………(1分)
W = Pt = 550×360 = 1.98×105(J) …………………………(1分)
η= …………………………………(1分)
…………………………………(1分)
(3)当加热时,S闭合,R1短路,得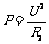 …………………………(1分)
…………………………(1分)
当保温时,S断开,R1与R2串联,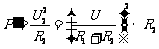 …………(1分)
…………(1分)
由题意得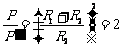 ………………………………(1分)
………………………………(1分)
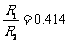 …………………………………………………………(1分)
…………………………………………………………(1分)
设计(7分)
8.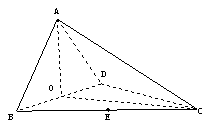 (2006福建文、理)如图,四面体ABCD中,O、E分别是BD、BC的中点,
(2006福建文、理)如图,四面体ABCD中,O、E分别是BD、BC的中点,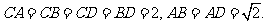
(I)求证: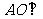 平面BCD; (II)求异面直线AB与CD所成角的大小;
平面BCD; (II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
7.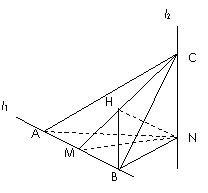 (2006全国Ⅰ卷文、理)如图,
(2006全国Ⅰ卷文、理)如图, 、
、 是互相垂直的异面直线,MN是它们的公垂线段.点A、B在
是互相垂直的异面直线,MN是它们的公垂线段.点A、B在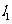 上,C在
上,C在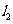 上,
上,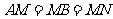 。 (Ⅰ)证明AC⊥NB;
。 (Ⅰ)证明AC⊥NB;
(Ⅱ)若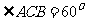 ,求
,求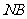 与平面ABC所成角的余弦值。
与平面ABC所成角的余弦值。
6.(2007四川理)如图,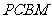 是直角梯形,∠
是直角梯形,∠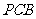 =90°,
=90°,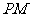 ∥
∥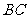 ,
,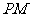 =1,
=1,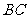 =2,又
=2,又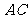 =1,∠
=1,∠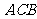 =120°,
=120°,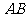 ⊥
⊥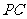 ,直线
,直线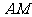 与直线
与直线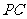 所成的角为60°.
所成的角为60°.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面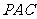 ⊥平面
⊥平面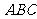 ; (Ⅱ)求二面角
; (Ⅱ)求二面角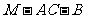 的大小;
的大小;
(Ⅲ)求三棱锥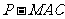 的体积.
的体积.
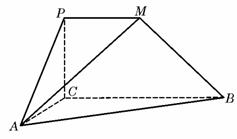
5.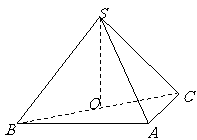 (2007海南、宁夏理)如图,在三棱锥
(2007海南、宁夏理)如图,在三棱锥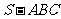 中,侧面
中,侧面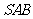 与侧面
与侧面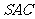 均为等边三角形,
均为等边三角形,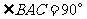 ,
, 为
为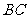 中点. (Ⅰ)证明:
中点. (Ⅰ)证明: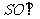 平面
平面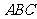 ;
;
(Ⅱ)求二面角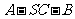 的余弦值.
的余弦值.
4.(2007安徽文、理)如图,在六面体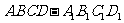 中,四边形ABCD是边长为2的正方形,四边形
中,四边形ABCD是边长为2的正方形,四边形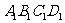 是边长为1的正方形,
是边长为1的正方形,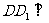 平面
平面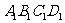 ,
,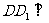 平面ABCD,DD1=2。
平面ABCD,DD1=2。
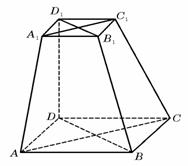 (Ⅰ)求证:
(Ⅰ)求证: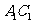 与AC共面,
与AC共面,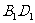 与BD共面.
与BD共面.
(Ⅱ)求证:平面
(Ⅲ)求二面角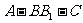 的大小.
的大小.
3.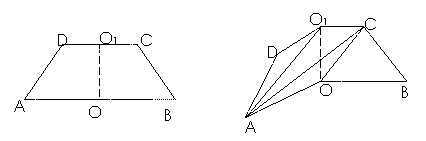 (2005湖南文、理)如图1,已知ABCD是上、下底边长分别为2和6,高为
(2005湖南文、理)如图1,已知ABCD是上、下底边长分别为2和6,高为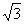 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2。
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2。
(Ⅰ)证明:AC⊥BO1; (Ⅱ)求二面角O-AC-O1的大小。
2.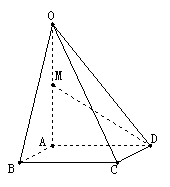 (2008安徽文)如图,在四棱锥
(2008安徽文)如图,在四棱锥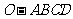 中,底面
中,底面 四边长为1的 菱形,
四边长为1的 菱形,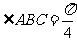 ,
,  ,
, 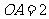 ,
,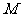 为
为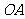 的中点。
的中点。
(Ⅰ)求异面直线AB与MD所成角的大小 ;
;
(Ⅱ)求点B到平面OCD的距离。
1.(2008海南、宁夏理)如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°。
 (1)求DP与CC1所成角的大小;(2)求DP与平面AA1D1D所成角的大小。
(1)求DP与CC1所成角的大小;(2)求DP与平面AA1D1D所成角的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com