
6.下列说法不符合递变规律的是
A.F2、Cl2、Br2、I2和H2反应激烈程度递减
B.HF、HCl、HBr、HI热稳定性减小
C.F2、Cl2、Br2、I2的氧化性递增
D.F-、Cl-、Br-、I- 失电子能力递增
3. 在酸性无色溶液中,下列各离子组能大量共存的是
A.K+、Na+、SO42-、Cl- B.Cu2+、Al3+、Cl-、SO42- C.Fe2+、I-、Cl-、CO32- D.Ag+、Na+、NO3-、Cl- 4、下列离子方程式书写不正确的是 A.氯水和碘化钾反应:Cl2+2I-=2Cl-+I2 B.二氧化锰和盐酸制氯气:MnO2+4H++2Cl-=Mn2++Cl2↑+2H2O C.氢氧化钙溶液吸收氯气:Cl2+2OH-=Cl-+ClO-+H2O D.氯气和水反应:Cl2+H2O=2H++Cl-+ClO- 5. 下列关于氯水的叙述正确的是
A.新制氯水中只含Cl2和H2O分子
B.新制氯水可使蓝色石蕊试纸先变红后褪色
C.光照氯水有气泡逸出该气体是Cl2
D.氯水放置数天后PH变大
2. 根据阿伏加德罗定律,下列叙述中正确的是
A.同温同压下Cl2和NH3的体积之比等于摩尔质量之比
B.同温同压下Cl2和NH3的物质的量之比等于密度之比
C.同温同压下Cl2和NH3的摩尔质量之比等于密度之比
D.同温同压下Cl2和NH3的摩尔质量之比等于压强之比
1. 下列物质中在空气中能稳定存在的是( )
A.氯水 B.氧化钠
C.生石灰 D.食盐
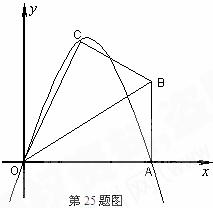
25.(本题满分12分)已知:在Rt△ABO中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为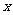 轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;(3分)
(2)若抛物线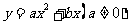 经过C、A两点,求此抛物线的解析式;(4分)
经过C、A两点,求此抛物线的解析式;(4分)
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作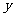 轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (5分)
轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (5分)
|
[答案]25.(1)过点C作CH⊥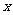 轴,垂足为H, ∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2 ∴OB=4,OA=
轴,垂足为H, ∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2 ∴OB=4,OA=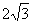 ,由折叠知,∠COB=300,OC=OA=
,由折叠知,∠COB=300,OC=OA=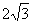
∴∠COH=600,OH=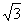 ,CH=3 ∴C点坐标为(
,CH=3 ∴C点坐标为(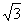 ,3)
,3)
(2)∵抛物线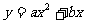 (
(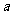 ≠0)经过C(
≠0)经过C(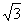 ,3)、A(
,3)、A(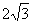 ,0)两点
,0)两点
∴ 解得:
解得: 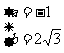
∴此抛物线的解析式为: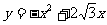
(3)存在. 因为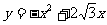 的顶点坐标为(
的顶点坐标为(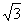 ,3)即为点C,MP⊥
,3)即为点C,MP⊥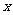 轴,设垂足为N,PN=
轴,设垂足为N,PN=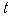 ,因为∠BOA=300,所以ON=
,因为∠BOA=300,所以ON=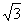
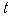 , ∴P(
, ∴P(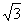
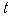 ,
,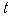 )
)
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E,把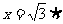 代入
代入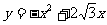 得:
得: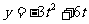 ,∴ M(
,∴ M(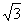
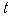 ,
,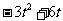 ),E(
),E(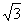 ,
,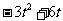 ) 同理:Q(
) 同理:Q(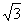 ,
,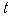 ),D(
),D(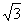 ,1), 要使四边形CDPM为等腰梯形,只需CE=QD
,1), 要使四边形CDPM为等腰梯形,只需CE=QD
即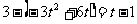 ,解得:
,解得: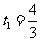 ,
,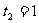 (舍), ∴ P点坐标为(
(舍), ∴ P点坐标为(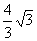 ,
,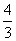 )
)
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(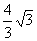 ,
,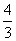 )
)

|

|
版权所有:()
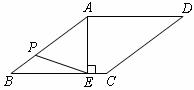
24.(8分)如图,在菱形ABCD中,AE⊥BC,E为垂足,cosB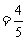 ,EC=2,
,EC=2,
⑴求菱形ABCD的边长.(4分)
⑵若P是AB边上的一个动点,则线段EP的长度的最小值是多少? (4分)
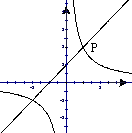
22.(8分)已知一次函数y=x+m与反比例函数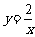 的图象在第一象限的交点为P(t ,2) 。
的图象在第一象限的交点为P(t ,2) 。
(1) 求t及m的值;
(2) 直接写出x在什么范围内一次函数的值大于反比例函数的值(不需要求解过程)。
21、(6分)解方程 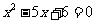
20、(6分)解不等式组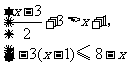
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com