
3. 汽车由甲地从静止出发沿平直公路驶向乙地停下。在这段时间内,汽车可做匀速运动,也可做加速度为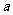 匀变速运动。已知甲、乙两地相距S,那么要使汽车从甲地到乙地所用时间最短,汽车应如何运动?最短时间为多少?
匀变速运动。已知甲、乙两地相距S,那么要使汽车从甲地到乙地所用时间最短,汽车应如何运动?最短时间为多少?
[解析]该题属于运动学极值问题,可用公式法建立方程,然后利用二次函数求极值。下面用速度图像求解:依据汽车运动特征(匀加速、匀速、匀减速)可作如下速度图像。因位移S恒定且等于梯形的“面积”,要使时间最短,汽车应无匀速运动过程,即汽车先做匀加速运动再做匀减速运动。
 设最短时间为
设最短时间为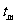 ,最大速度为
,最大速度为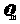 ,则据
,则据
 ,
,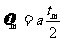 ,得
,得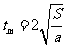
2. 一物体做加速直线运动,依次通过A、B、C三点,AB=BC。物体在AB段加速度为a1,在BC段加速度为a2,且物体在B点的速度为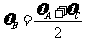 ,则
,则
 A.a1> a2
B.a1= a2 C.a1<
a2 D.不能确定
A.a1> a2
B.a1= a2 C.a1<
a2 D.不能确定
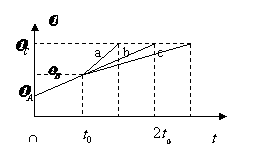
[解析]依题意作出物体的速度图像如图所示。图线下方所围成的面积在数值上等于物体的位移,由几何知识知:图线b、c不满足AB=BC,图线a可满足之。又斜率表示加速度,所以a1<a2。
1. (2007高考全国理综Ⅰ)甲乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持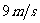 的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机,需在接力区前适当的位置设置标记。在某次练习中,甲在接力区前
的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机,需在接力区前适当的位置设置标记。在某次练习中,甲在接力区前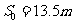 处作了标记,并以
处作了标记,并以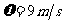 的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒。已知接力区的长度为
的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒。已知接力区的长度为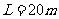 。求:⑴此次练习中乙在接棒前的加速度
。求:⑴此次练习中乙在接棒前的加速度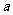 。
。
⑵在完成交接棒时乙离接力区末端的距离。
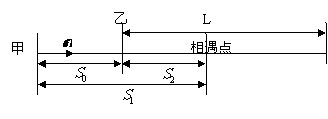 [解析]该题实质上是追及、相遇问题,其物理情景同学们比较熟悉,对参加过接力赛的同学来说,大多都能正确画出如下过程示意图。
[解析]该题实质上是追及、相遇问题,其物理情景同学们比较熟悉,对参加过接力赛的同学来说,大多都能正确画出如下过程示意图。
依据甲、乙两运动员的运动过程所
作速度图像如图所示。
⑴由于追上时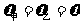 ,由图知
,由图知
三角形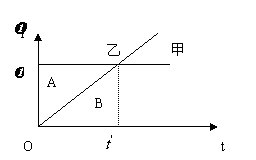 A的“面积”即为甲“发口令”时二者间距
A的“面积”即为甲“发口令”时二者间距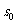
(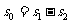 ),三角形B的“面积” 为甲、乙
),三角形B的“面积” 为甲、乙
相遇时乙的位移且 ,
,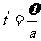 ,
,
所以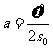 。
。
⑵在完成交接棒时乙离接力区末端的距离 。
。
[答案]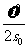 ;
;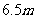 。
。
7.巧用匀变速直线运动的推论解题
①某段时间内的平均速度 = 这段时间中时刻的即时速度
②连续相等时间间隔内的位移差为一个恒量
③位移=平均速度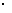 时间
时间
6.用比例法解题
5.应用运动学图象解题
4.逆向思维法解题
3.利用运动的对称性解题
2.巧选参考系求解运动学问题
1.平均速度的求解及其方法应用
① 用定义式: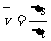 普遍适用于各种运动;②
普遍适用于各种运动;② 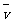 =
= 只适用于加速度恒定的匀变速直线运动
只适用于加速度恒定的匀变速直线运动
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com