
5. 苯氯乙酮是一种具有荷花香味的有机物,其结构简式为

请回答下列问题:
(1)苯氯乙酮的分子式为 。
(2)苯氯乙酮可能发生的化学反应类型有 (填选字母)。
a.加成反应 b.取代反应 c.消去反应 d.水解反应 e.银镜反应
(3)苯氯乙酮的同分异构体有多种,请写出同时符合下列三个条件的任意两种同分异构题的结构简式:
①分子内有苯环但不含甲基; ②氯原子与链烃基直接相连
③能发生银镜反应。
、 。
|
|||||
|
|||||
|
|||||
 (4)已知:①RCHCH2OH
R—C—COOH
(4)已知:①RCHCH2OH
R—C—COOH
②通常状况下氯苯在氢氧化钠水溶液中不能发生水解反应。
 某已知酮的一种同分异构体M,可发生银镜反应,能用于合成杀菌剂F,D的结构
某已知酮的一种同分异构体M,可发生银镜反应,能用于合成杀菌剂F,D的结构
 简式是:
,由M→F的转化关系如下;
简式是:
,由M→F的转化关系如下;
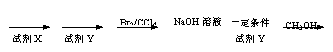
|

 M
A
B
C
D
E
M
A
B
C
D
E
请回答:
①M的结构简式为 ,D中含有官能团名称为 。
②A→B的化学反应方程式为 ;
E→D的化学反应方程式为 。
③C与NaOH醇溶液反应,所得产物的分子式为C8H5Cl,则该产物的结构简式为
。
4. 为有机物A的结构简式,可以通过不同的反应制得下列物质。
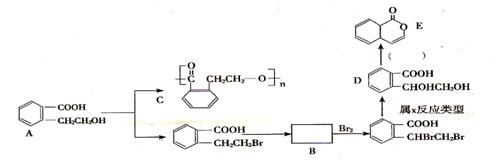
(1)写出A → C的化学方程式: 。
(2)推断B物质的结构简式 ;X反应类型是 ;由 D → E 所需的试剂是 。
(3)R物质属于A 的同分异构体,其性质如下:
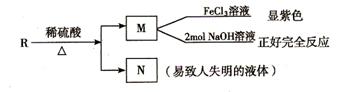
试写出符合条件的R的同分异构体的结构简式(任写两种) : ; 。
3. 乙醇是一种重要的化工产品、化工原料和应用前景广阔的可再生能源。
(1)以玉米及其他含糖类农副产品等为原料,经发酵、蒸馏制得乙醇。多糖经过水解转化为葡萄糖,葡萄糖受到酒化酶的作用转化为乙醇。请写出葡萄糖转化为乙醇的化学方程式 。
(2)已知:C2H5OH(l)+3O2(g)=2CO(g)+3H2O(l);△H=-1367kJ/mol。玉米中淀粉和纤维素的含量为81%,,由玉米转化为乙醇时,原料总利用率为80%,则1000g玉米制得的乙醇完全燃烧后放出的热量为 kJ。
(3)香豆素是一种用途广泛的香料,它可以利用乙醇和B通过以下途径合成。已知B的分子式为C7H6O2,它遇到FeCl3溶液显紫色,其苯环上的一氯代物有4种。
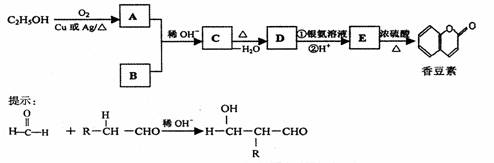
回答下列问题:
(1)D的结构简式 。
(2)C→D反应类型 。
(3)E中存在的含氧官能团名称是 。
(4)写出E→香豆素的化学方程式 。
(5)B有多种同分异构体,写出其中苯环上只有一个侧链的所有同分异构体的结构简式
。
(6)有关香豆素的说法正确的是 ( )
A.1mol香豆素能与2mol NaOH溶液发生反应
B.香豆素既能使溴水褪色又能使酸性高锰酸钾褪色
C.1mol香豆素能与5mol氢气发生加成反应
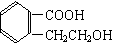 D.香豆素既属于酯类物质,也属于芳香族化合物
D.香豆素既属于酯类物质,也属于芳香族化合物
2. 某药物有效成分为有机物M,跟(CH3)2SO4反应生成有机物A.二者的结构简式如图

试回答:
(1)有机物M的分子式为 ,1mol有机物M跟浓溴水反应时最多消耗 mol Br2;有机物A不能发生的化学反应有 (用番号表示)。
①加成反应 ②取代反应 ③消去反应 ④水解反应 ⑤银镜反应
(2)有机物A能发生如下转化:
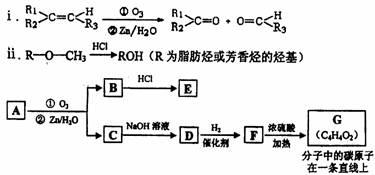 提示:
提示:
①C→D的化学方程式为 。
②写出结构简式F ,G 。
③写出其中两种符合下列条件的E的同分异构体的结构简式。
a.遇FeCl3溶液呈紫色
b.不能发生水解反应,能发生银镜反应
c.苯环上的一氯取代物只有一种,分子中无甲基
d.苯环上有四个取代基
1. 已知两个羟基同时连在同一碳原子上的结构是不稳定的,它要发生脱水反应:

现有分子式为C9H8O2X2(X为一未知元素)的物质M,可在一定条件下发生下述一系
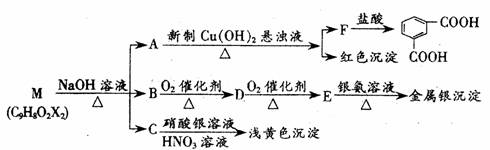 列反应:
列反应:
试回答下列问题:
(1)X为 (填元素符号);其判断依据是 。
(2)A用盐酸酸化所得的物质中所含的官能团的名称为 ,
(3)M的结构简式为 。
(4)写出下列反应的化学方程式:
①B→D: 。
②A与新制Cu(OH2)悬浊液反应: 。
反应的类型为 。
③B+E: 。
17. 抽象函数:抽象函数通常是指没有给出函数的具体的解析式,只给出了其它一些条件(如函数的定义域、单调性、奇偶性、解析递推式等)的函数问题。求解抽象函数问题的常用方法是:
(1)借鉴模型函数进行类比探究。几类常见的抽象函数 :
①正比例函数型: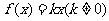 ---------------
---------------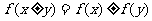 ;
;
②幂函数型: --------------
--------------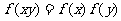 ,
, ;
;
③指数函数型: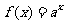 ------------
------------ ,
,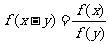 ;
;
④对数函数型: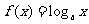 -----
-----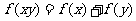 ,
, ;
;
⑤三角函数型: -----
----- 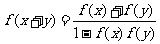 。如已知
。如已知 是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则
是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则 ____(答:0)
____(答:0)
(2)利用函数的性质(如奇偶性、单调性、周期性、对称性等)进行演绎探究:如(1)设函数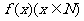 表示
表示 除以3的余数,则对任意的
除以3的余数,则对任意的 ,都有 A、
,都有 A、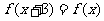 B、
B、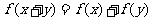 C、
C、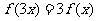 D、
D、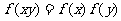 (答:A);(2)设
(答:A);(2)设 是定义在实数集R上的函数,且满足
是定义在实数集R上的函数,且满足 ,如果
,如果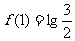 ,
, ,求
,求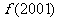 (答:1);(3)如设
(答:1);(3)如设 是定义在
是定义在 上的奇函数,且
上的奇函数,且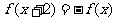 ,证明:直线
,证明:直线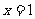 是函数
是函数 图象的一条对称轴;(4)已知定义域为
图象的一条对称轴;(4)已知定义域为 的函数
的函数 满足
满足 ,且当
,且当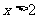 时,
时, 单调递增。如果
单调递增。如果 ,且
,且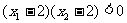 ,则
,则 的值的符号是____(答:负数)
的值的符号是____(答:负数)
(3)利用一些方法(如赋值法(令 =0或1,求出
=0或1,求出 或
或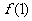 、令
、令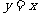 或
或 等)、递推法、反证法等)进行逻辑探究。如(1)若
等)、递推法、反证法等)进行逻辑探究。如(1)若 ,
, 满足
满足
 ,则
,则 的奇偶性是______(答:奇函数);(2)若
的奇偶性是______(答:奇函数);(2)若 ,
, 满足
满足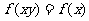
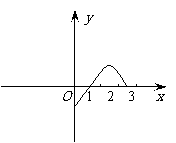
 ,则
,则 的奇偶性是______(答:偶函数);(3)已知
的奇偶性是______(答:偶函数);(3)已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当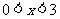 时,
时, 的图像如右图所示,那么不等式
的图像如右图所示,那么不等式 的解集是_____________(答:
的解集是_____________(答: );(4)设
);(4)设 的定义域为
的定义域为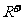 ,对任意
,对任意 ,都有
,都有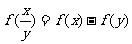 ,且
,且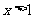 时,
时,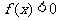 ,又
,又 ,①求证
,①求证 为减函数;②解不等式
为减函数;②解不等式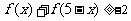 .(答:
.(答: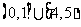 ).
).
16. 函数的应用。(1)求解数学应用题的一般步骤:①审题--认真读题,确切理解题意,明确问题的实际背景,寻找各量之间的内存联系;②建模--通过抽象概括,将实际问题转化为相应的数学问题,别忘了注上符合实际意义的定义域;③解模--求解所得的数学问题;④回归--将所解得的数学结果,回归到实际问题中去。(2)常见的函数模型有:①建立一次函数或二次函数模型;②建立分段函数模型;③建立指数函数模型;④建立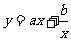 型。
型。
15. 指数、对数值的大小比较:(1)化同底后利用函数的单调性;(2)作差或作商法;(3)利用中间量(0或1);(4)化同指数(或同真数)后利用图象比较。
14.指数式、对数式:
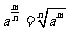 ,
, ,,
,,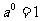 ,
,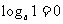 ,
, ,
,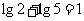 ,
,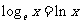 ,
, ,
, ,
,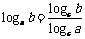 ,
, 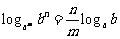 。如(1)
。如(1)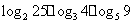 的值为________(答:8);(2)
的值为________(答:8);(2)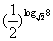 的值为________(答:
的值为________(答: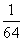 )
)
13. 函数的周期性。
(1)类比“三角函数图像”得:
①若 图像有两条对称轴
图像有两条对称轴 ,则
,则 必是周期函数,且一周期为
必是周期函数,且一周期为 ;
;
②若 图像有两个对称中心
图像有两个对称中心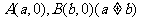 ,则
,则 是周期函数,且一周期为
是周期函数,且一周期为 ;
;
③如果函数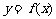 的图像有一个对称中心
的图像有一个对称中心 和一条对称轴
和一条对称轴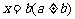 ,则函数
,则函数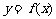 必是周期函数,且一周期为
必是周期函数,且一周期为 ;
;
如已知定义在 上的函数
上的函数 是以2为周期的奇函数,则方程
是以2为周期的奇函数,则方程 在
在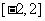 上至少有__________个实数根(答:5)
上至少有__________个实数根(答:5)
(2)由周期函数的定义“函数 满足
满足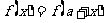
 ,则
,则 是周期为
是周期为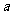 的周期函数”得:
的周期函数”得:
①函数 满足
满足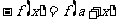 ,则
,则 是周期为2
是周期为2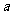 的周期函数;
的周期函数;
②若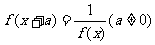 恒成立,则
恒成立,则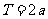 ;
;
③若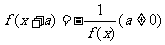 恒成立,则
恒成立,则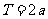 .
.
如(1)
设 是
是 上的奇函数,
上的奇函数,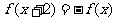 ,当
,当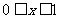 时,
时, ,则
,则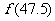 等于_____(答:
等于_____(答: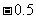 );(2)定义在
);(2)定义在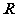 上的偶函数
上的偶函数 满足
满足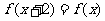 ,且在
,且在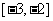 上是减函数,若
上是减函数,若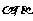 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则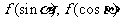 的大小关系为_________(答:
的大小关系为_________(答: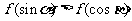 );(3)已知
);(3)已知 是偶函数,且
是偶函数,且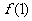 =993,
=993,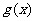 =
=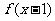 是奇函数,求
是奇函数,求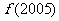 的值(答:993);(4)设
的值(答:993);(4)设 是定义域为R的函数,且
是定义域为R的函数,且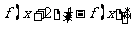
 ,又
,又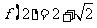 ,则
,则 = (答:
= (答: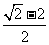 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com